接触锁相环的缘由
学电力电子,尤其是新能源光伏或风电的并网运行需要同步电网,需要锁相环来同步相位信息。对于电力驱动领域,无位置传感器电力驱动有运用锁相环的需求。我最近研究的电力驱动内容也有需求锁定一个未知信号的相位,因此需要了解并使用锁相环。大概花了一个月的时间来学习锁相环,对锁相环的基本原理有了一定的了解。尤其是自己明白原理后,看其他文献就容易理解了。不会像最开始学习锁相环阶段,看着锁相环就头大,头晕。实际锁相环的基本原理并不难,尤其是公式推导过程(公式偏多),不要抵触,多花点时间就可以掌握。接下来首先介绍锁相环的需要完成的目标。
Phase Locked Loop 的目标
PLL 全称为 Phase Locked Loop,中文名把它叫做锁相环。PLL 的基本功能是跟踪、锁定交流信号的相位,且在必要时还可以提供有关信号的频率和幅值1。
乘法鉴相锁相环
基于乘法鉴相器的锁相环是最基础的一种。主要参看文献《PWM 整流器及其控制》来学习锁相环,以此来掌握核心的概念,并加深对锁相环的理解。
锁相环的基本构成
基本锁相环的闭环控制回路一般含有鉴相器(PD)、环路滤波器(LF)和压控振荡器(VCO)这三种结构,如图1所示。乘法鉴相锁相环是指鉴相器采用乘法器的锁相环。
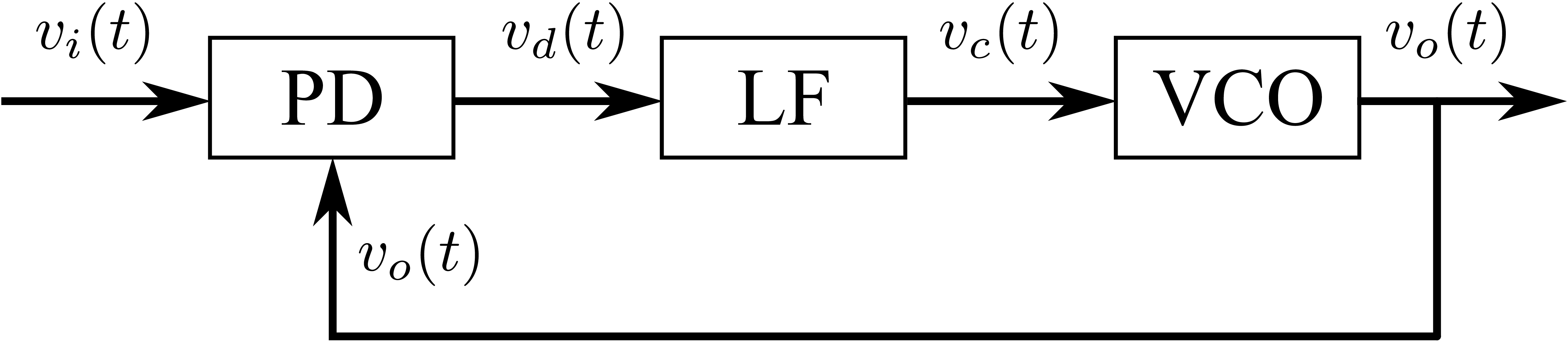
- 鉴相器:比较输入信号\(v_{i}(t)\)和输出信号\(v_{o}(t)\)的相位。
- 环路滤波器:滤除误差信号\(v_{d}(t)\)的二次谐波分量和噪声。
- 压控振荡器:完成电压和频率的变换,即压控振荡器的输出信号的频率与误差信号\(v_{d}(t)\)的大小成正比。
接下来就分别分析锁相环的三个基本单元鉴相器、环路滤波器、压控振荡器(PD,LP,VCO)的功能和数学模型。其中,锁相环最核心的部分是鉴相器。鉴相器的核心就是实现输入信号\(v_{i}(t)\)相位与锁相环输出信号\(v_{o}(t)\)的相位的差。换句话说,只要能实现输入信号与锁相环输出信号的相位差,就可以作为锁相环的鉴相器。只要理解锁相环中鉴相器原理,那么这个锁相环核心部分就理解了。
乘法鉴相器 PD
实际要分析的是为什么乘法器能实现相位的比较? 带着这个问题去理解乘法鉴相器。
定义输入信号: \[ \begin{equation} v_{i}(t) = V_i \sin[\omega_i t +\theta_i(t)] \end{equation} \]
定义输出信号: \[ \begin{equation} v_{o}(t) = V_o \cos[\omega_o t +\theta_o(t)] \end{equation} \]
这样一看这两个信号就含有 \(\omega_i\)、\(\omega_o\)、\(\theta_{i}(t)\)、 \(\theta_o(t)\)、\(V_i\) 和 \(V_o\),总共6个变量,看来需要简化简化,方便后续的分析。
注意:输入输出信号为两正交信号(\(\sin, \cos\))
以 \(\omega_o\) 为参考频率,重新定义输入信号的瞬时相位:
\[ \begin{equation} [\omega_i t + \theta_i(t)] = \omega_o t + [(\omega_i-\omega_o)t + \theta_i(t)] = \omega_o t + \theta_{1}(t) \end{equation} \]
其中,\(\theta_{1}(t) =(\omega_i-\omega_o)t + \theta_i(t)=\Delta \omega_o t + \theta_i(t)\)
输出信号的瞬时相位:
\[ \begin{equation} \omega_o t + \theta_o(t) = \omega_o t + \theta_2(t) \end{equation} \]
其中,\(\theta_2(t)=\theta_o(t)\)。
简化后的输入输出信号表达式: \[ \begin{equation} \left\{ \begin{aligned} \label{eq:input and out signal} v_i(t) &= V_i \sin [\omega_o t + \theta_{1}(t)]\\ v_o(t) &= V_o \cos [\omega_o t + \theta_{2}(t)]\\ \end{aligned} \right. \end{equation} \]
和最初定义相比,减少了一个频率变量\(\omega_i\)。
乘法鉴相器结构框图,如图2所示,简单的数学表达式为\(v_d(t)=K_m v_i(t) v_o(t)\),其中\(K_m\) 为乘法器的比列系数。
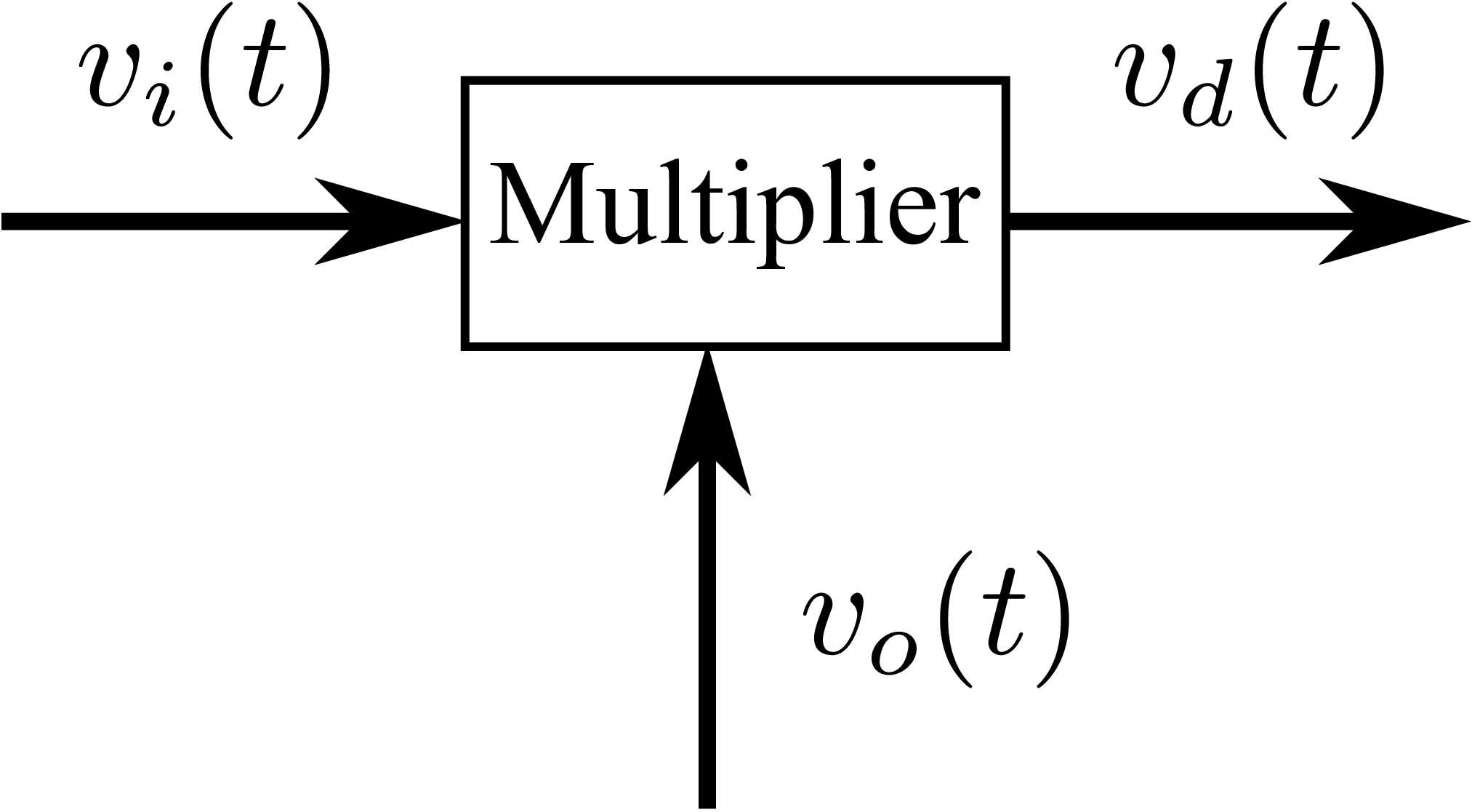
再用个积化和差公式:
\[ \begin{equation} \sin\alpha \cdot \cos\beta = \frac{1}{2} [\sin(\alpha+\beta)+\sin(\alpha-\beta) ]\\ \end{equation} \]
在乘法鉴相器数学表达式中,应用三角函数积化和差公式化简过程:
\[ \begin{equation} \label{eq:complex output signal} \begin{aligned} v_d(t) & = K_m v_i(t) v_o(t)\\ & = K_m V_i V_o \cos [\omega_o t + \theta_{2}(t)] \sin [\omega_o t + \theta_{1}(t)]\\ & = \frac{1}{2} K_m V_i V_o \sin[2\omega_o t+ \theta_1(t)+\theta_2(t)]+\frac{1}{2} K_m V_i V_o \sin[\theta_1(t)-\theta_2(t)] \end{aligned} \end{equation} \]
其中,\(\frac{1}{2} K_m V_i V_o \sin[2\omega_o t+\theta_1(t)+\theta_2(t)]\) 含有二次谐波,需要设置一个低通滤波器将其滤除。
故公式\(\eqref{eq:complex output signal}\)可做进一步的简化,去掉二次谐波部分。
\[ \begin{equation} \label{eq:simple output singal} v_d(t)=\frac{1}{2} K_m V_i V_o\sin[\theta_1(t)-\theta_2(t)] \end{equation} \]
看公式\(\eqref{eq:simple output singal}\) 中的 \(\theta_1(t)-\theta_2(t)\),这不是出现了两瞬时相位之差了吗?可以解决本小节最开始提出的问题。
"实际要分析的是为什么乘法器能实现相位的比较?"
进一步简化\(v_d(t)\)
定义瞬时相位差: \[ \begin{equation} \begin{aligned} \theta_e(t) &= \theta_1(t)-\theta_2(t)\\ &= \Delta \omega_o t + \theta_i(t) -\theta_o(t) \end{aligned} \end{equation} \]
定义幅值: \[ \begin{equation} V_d = \frac{1}{2} K_m V_i V_o \end{equation} \]
再进一步简化 \[ \begin{equation} v_d(t) = V_d \sin \theta_e(t) \end{equation} \]
这已经是最简化的形式了。
定义过零点的斜率为\(K_d\),把 \(K_d\)称为鉴相器的灵敏度。
\[ \begin{equation} K_d = \frac{\mathrm{d}v_d}{\mathrm{d}\theta_e}\bigg|_{\theta_e=0} =\frac{\mathrm{d}}{\mathrm{d}\theta_e}(V_d\sin\theta_e)\bigg|_{\theta_e=0} = Vd \end{equation} \]
故\(v_d(t)\)也可以写成:
\[ \begin{equation} v_d(t) = K_d \sin \theta_e(t) \end{equation} \]
这就是乘法鉴相器的数学模型,其结构图请见图3。
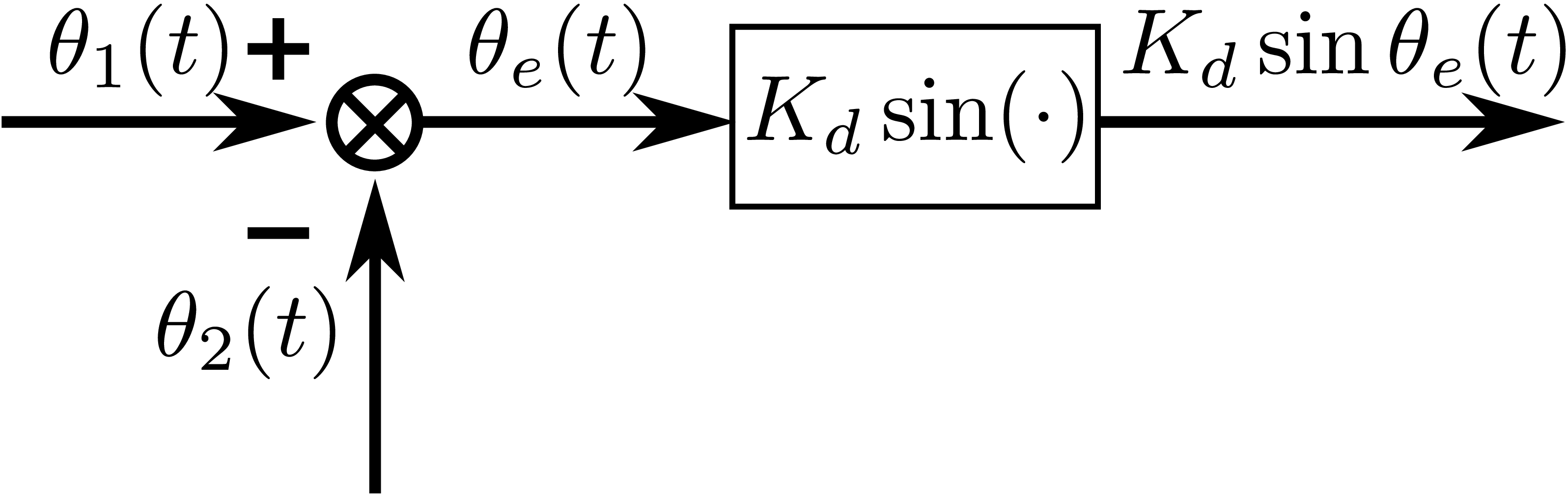
压控振荡器
何为压控振荡器?
压控振荡器的振荡频率\(\omega_v(t)\)随控制电压\(v_c(t)\)成正比(近似正比)变化。如图4所示为压控振荡器特性曲线。
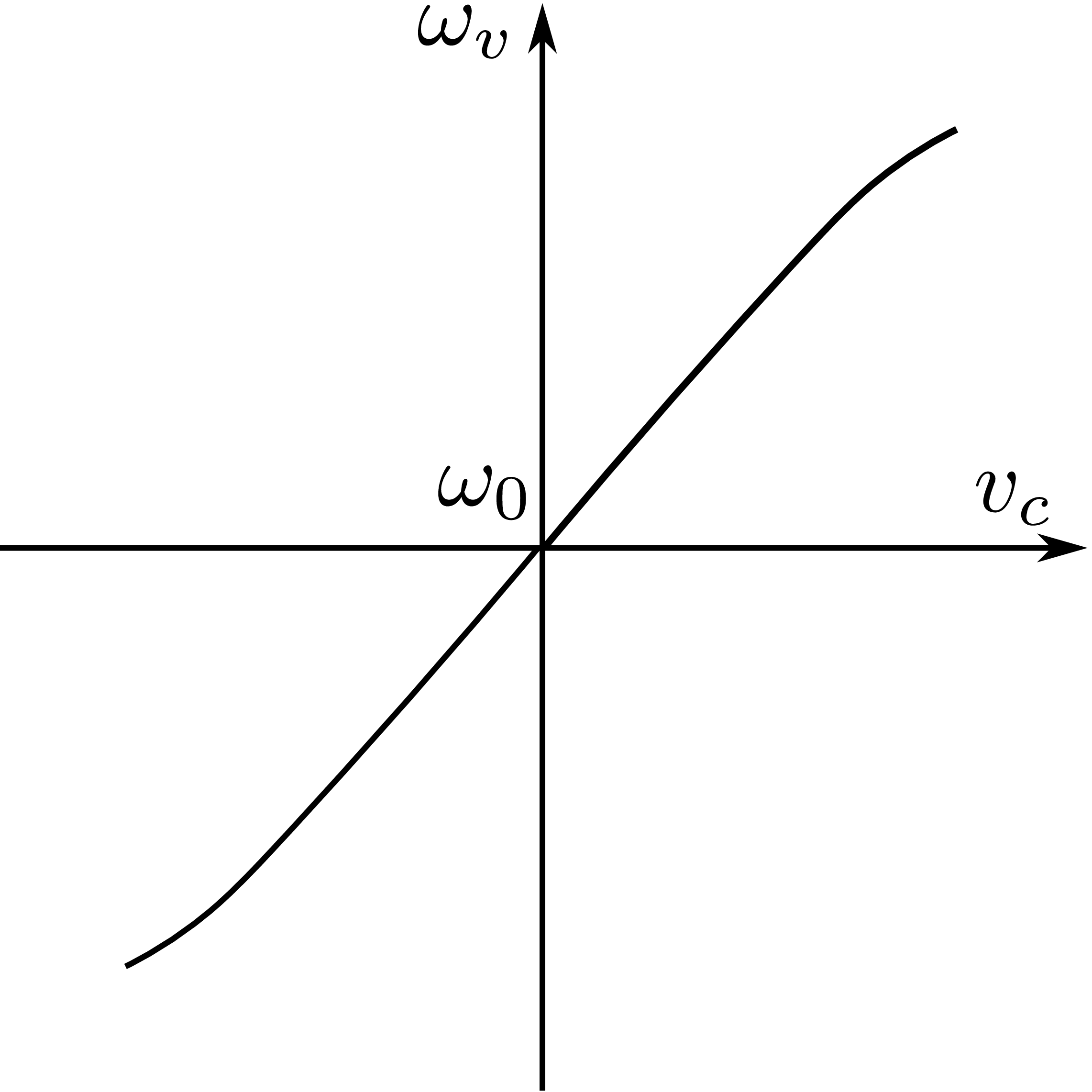
用数学表达式表示压控振荡器特性曲线: \[ \begin{equation} \label{eq:VCOCharacteristic} \omega_v(t)=\omega_0 + K_o v_c(t) \end{equation} \]
注意:\(\omega_0\) 与 \(\omega_o\) 区别,\(\omega_0\)一个是 VCO 固有振荡频率, \(\omega_o\) 是输出信号频率。
如图3所示,对鉴相器起作用的是瞬时相位\(\theta_2(t)\),不是瞬时角频率 \(\omega_v (t)\)。 \[ \begin{equation} \omega_o t + \theta_2(t)=\int_{0}^{t} \omega_v(t) d(t)= \omega_0 t + K_0 \int_{0}^{t} v_{c}(t) dt \end{equation} \]
\[ \begin{equation} \theta_2(t) = K_0 \int_{0}^{t} v_{c}(t) dt \end{equation} \]
这就是压控振荡器的数学模型,显然是一个积分器。定义微分算子 \(p=d/dt\)。 \[ \begin{equation} \theta_2(t) = K_0 \frac{v_{c}(t)}{p} \end{equation} \]
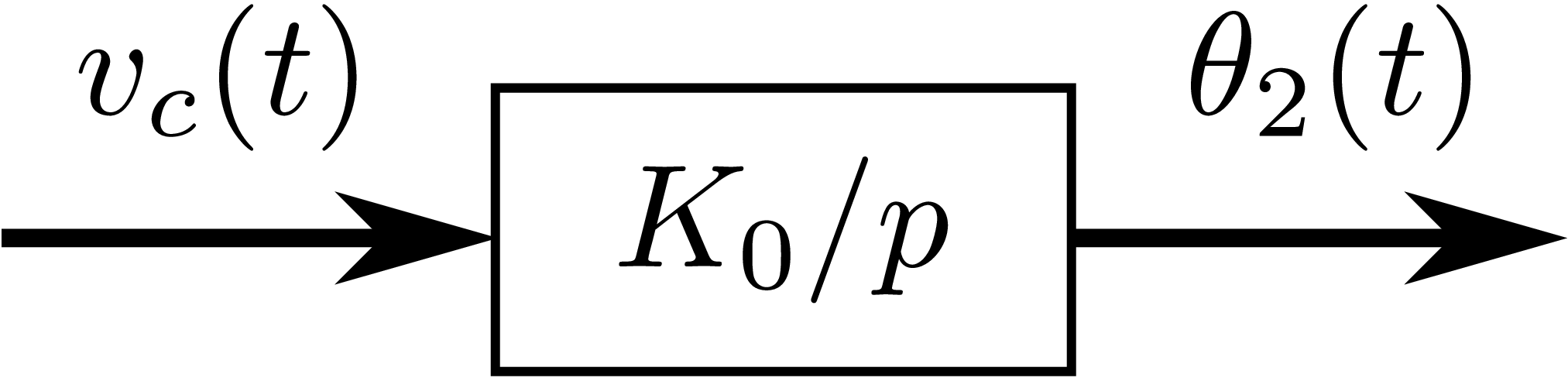
环路滤波器
环路滤波器的作用主要是用来滤除鉴相器输出信号的二次谐波分量和噪声。
环路滤波器的\(s\)域数学模型: \[ \begin{equation} V_c(s) = F(s) V_d(s) \end{equation} \]
换成微分算子的形式:
\[ \begin{equation} v_c(t)=F(p)v_d(t) \end{equation} \]
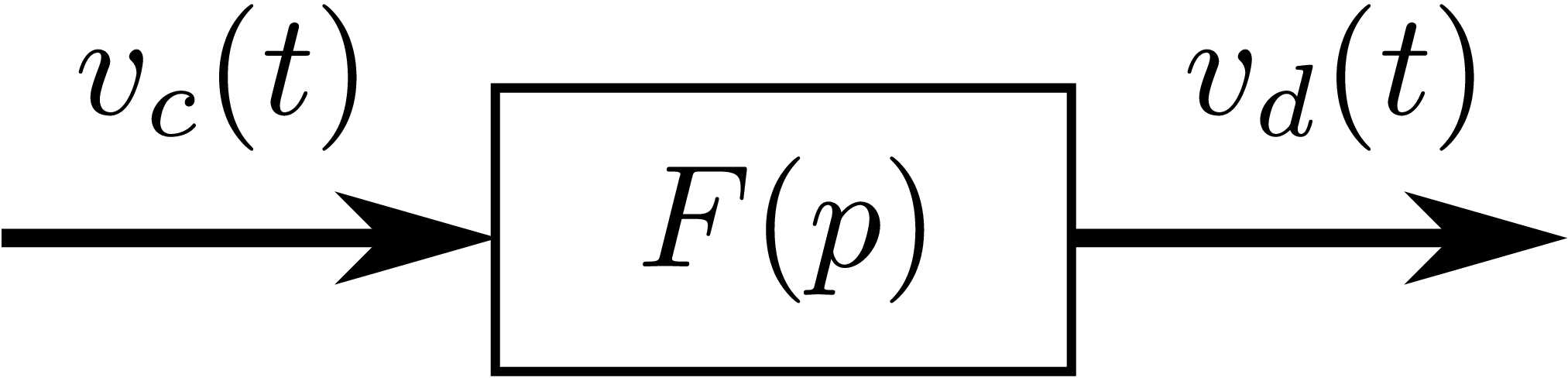
乘法鉴相器锁相环基本相位方程
根据前面三个基本单元的分析,可以综合成一个模型图,如图7所示。

\[ \begin{equation} \theta_e(t)=\theta_1(t) - \theta_2(t)=\theta_1(t) - K_0F(p) \frac{v_d(t)}{p} =\theta_1(t) - K_0 K_d F(p) \frac{1}{p} \sin \theta_e(t) \end{equation} \]
两端微分:
\[ \begin{equation} \frac{\mathrm{d}\theta_e(t)}{\mathrm{d}t}+K_0 K_d F(p) \sin \theta_e(t) = \frac{\mathrm{d}\theta_1(t)}{\mathrm{d}t} \end{equation} \]
锁相环锁定问题
当锁相环输入一个频率和相位不随时间变化的信号,即\(v_i(t)=V_i\sin(\omega_i t+\theta_i)\)。\(\omega_i\)与\(\theta_i\) 不随时间变化。
\[ \begin{equation} \frac{\mathrm{d}\theta_1(t)}{\mathrm{d}t} = \omega_i - \omega_o = \Delta \omega_o \end{equation} \]
简化基本相位方程:
\[ \begin{equation} \underbrace{\frac{\mathrm{d}\theta_e(t)}{\mathrm{d}t}}_{\omega_e} +\underbrace{K_0 K_d F(p) \sin \theta_e(t)}_{\omega_v-\omega_0} = \Delta \omega_o \end{equation} \]
参考锁相环的相位反馈图7和VCO特性方程\(\eqref{eq:VCOCharacteristic}\),可得
\[ \begin{equation} \label{eq:control frequencyi difference} \begin{aligned} K_0 K_d F(p) \sin \theta_e(t) & = K_0 F(p) [K_d\sin\theta_e(t)]\\ &= K_0 F(p) v_d(t)\\ &= K_0 v_c(t)\\ &= \omega_v - \omega_0 \end{aligned} \end{equation} \]
\(\omega_v - \omega_0\)称为控制频差,是压控振荡器受控制电压\(v_c(t)\)作用而产生的。
注意:\(\omega_0\) 与 \(\omega_o\) 区别,\(\omega_0\)一个是 VCO 固有振荡频率,\(\omega_o\) 是输出信号频率。
\(\frac{\mathrm{d}\theta_e(t)}{\mathrm{d}t}\) 可以用 \(\omega_e\) 代替,被称为瞬时频差。
\[ \begin{equation} \begin{aligned} \frac{\mathrm{d}\theta_e(t)}{\mathrm{d}t} = \frac{\mathrm{d}\theta_1(t)-\theta_2(t)}{\mathrm{d}t} \end{aligned} \end{equation} \]
书上的解释不清楚,下面是我按照自己理解,来解释整个锁相环的工作情况。
现在分析锁相环是如何实现频率的锁定和相位的锁定?
根据图7来分析锁定问题。假设存在某一时刻\(\theta_1(t)>\theta_2(t)\),\(0 <\theta_e(t)<\frac{\pi}{2}\),\(\theta_1(t)\) 与 \(\theta_2(t)\) 的差值在扩大,也就是说\(\theta_1(t)\)对应的角频率大于\(\theta_2(t)\) 的角频率。\(\theta_e(t)=\theta_1(t)-\theta_2(t)>0\) \(\uparrow\),那么 \(v_d(t)\) \(\uparrow\) ,那么 \(v_c(t)\) \(\uparrow\),那么对应 VCO 的输出信号频率增加\(\omega_v\),那么\(\theta_2(t)\)的频率在增加,以此来追上\(\theta_2(t)\)的频率,当 \(\theta_1(t)\)的频率和 \(\theta_2(t)\)的频率相等时,\(\theta_e(t)\)就是一个恒定值,整个闭环系统进入稳态。
现在的稳定状态是有输入输出信号是有相位差。为了实现相位偏差为零,可以在环路滤波器之后加一个PI,便可实现相位的零稳态误差。
经典的三相锁相环
经典的三相系统的锁相环主要参考文献 Operation of a phase locked loop system under distorted utility conditions2。
经典三相锁相环原理图
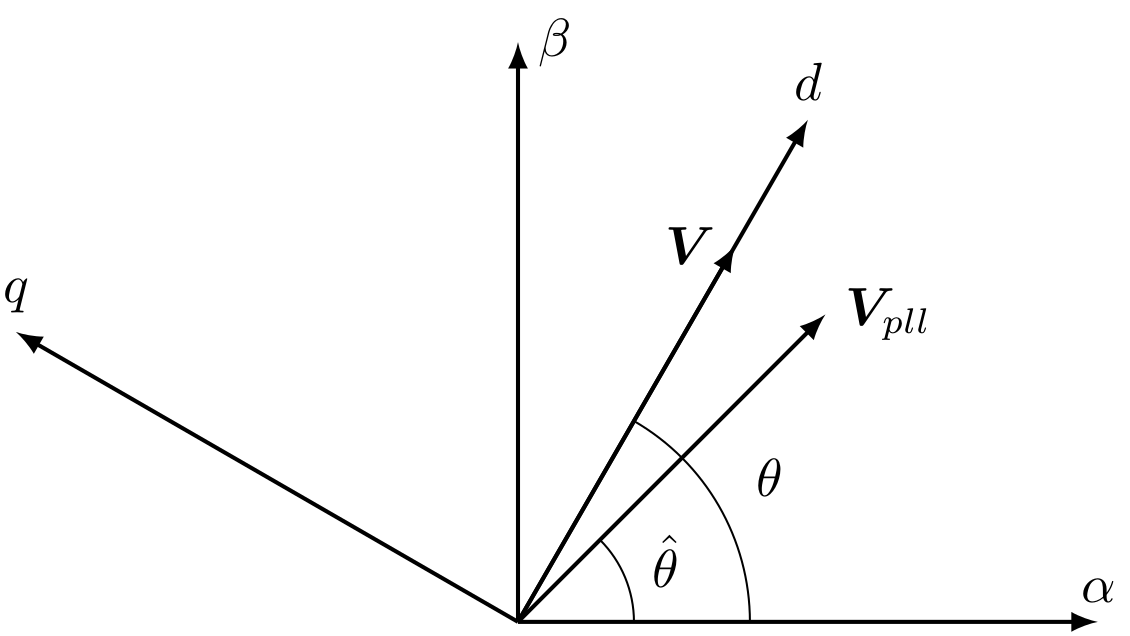
SSRF-SPLL矢量图8各变量定义:
- \(\mathbf{V}\) 实际电压矢量
- \(\mathbf{V}_{pll}\) 锁相环的输出电压矢量
- \(\theta\) 实际电压矢量的矢量角度
- \(\hat{\theta}\) 锁相环输出的电压矢量角度
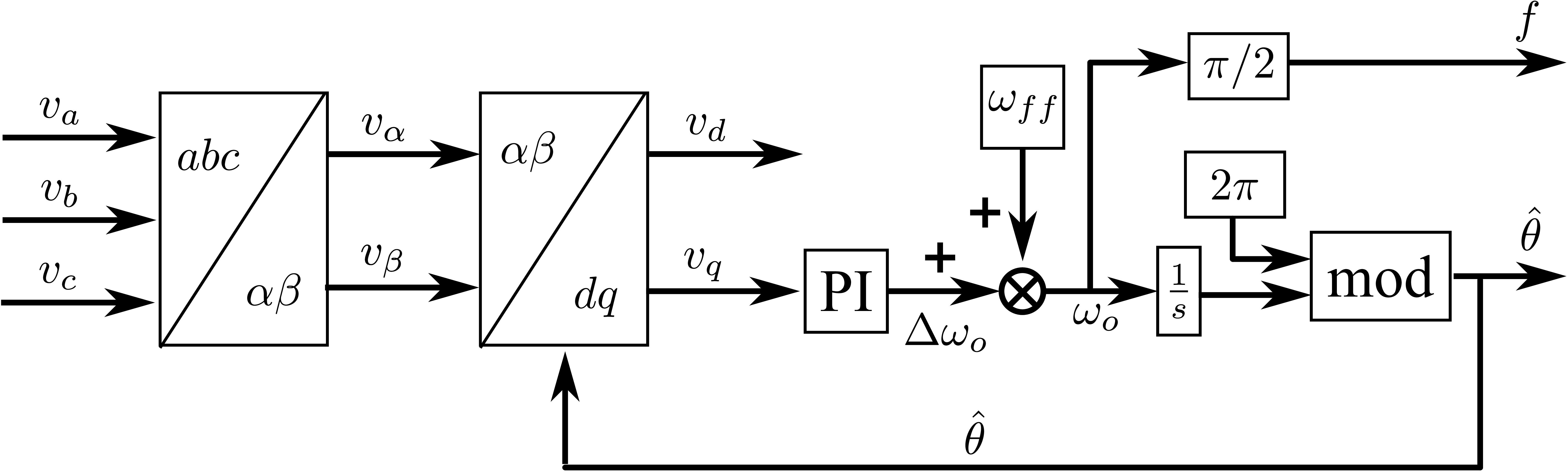
\(\omega_{ff}\) 是检测电压的额定频率,那这个物理量的作用是什么?主要是设置一个检测信号的额定频率,实际信号的频率是在这个频率\(\omega_{ff}\)上下波动,主要降低PI控制器输出的压力,这样PI输出就没必要和额定频率一样大,只需一个较小的量\(\Delta \omega_o\)即可。同时,\(\omega_{ff}\)给系统的频率一个初始值,有维持系统稳定的作用(不必要从0直接突变到\(\omega_{ff}\)附近,而是直接在\(\omega_{ff}\)附近变化)。
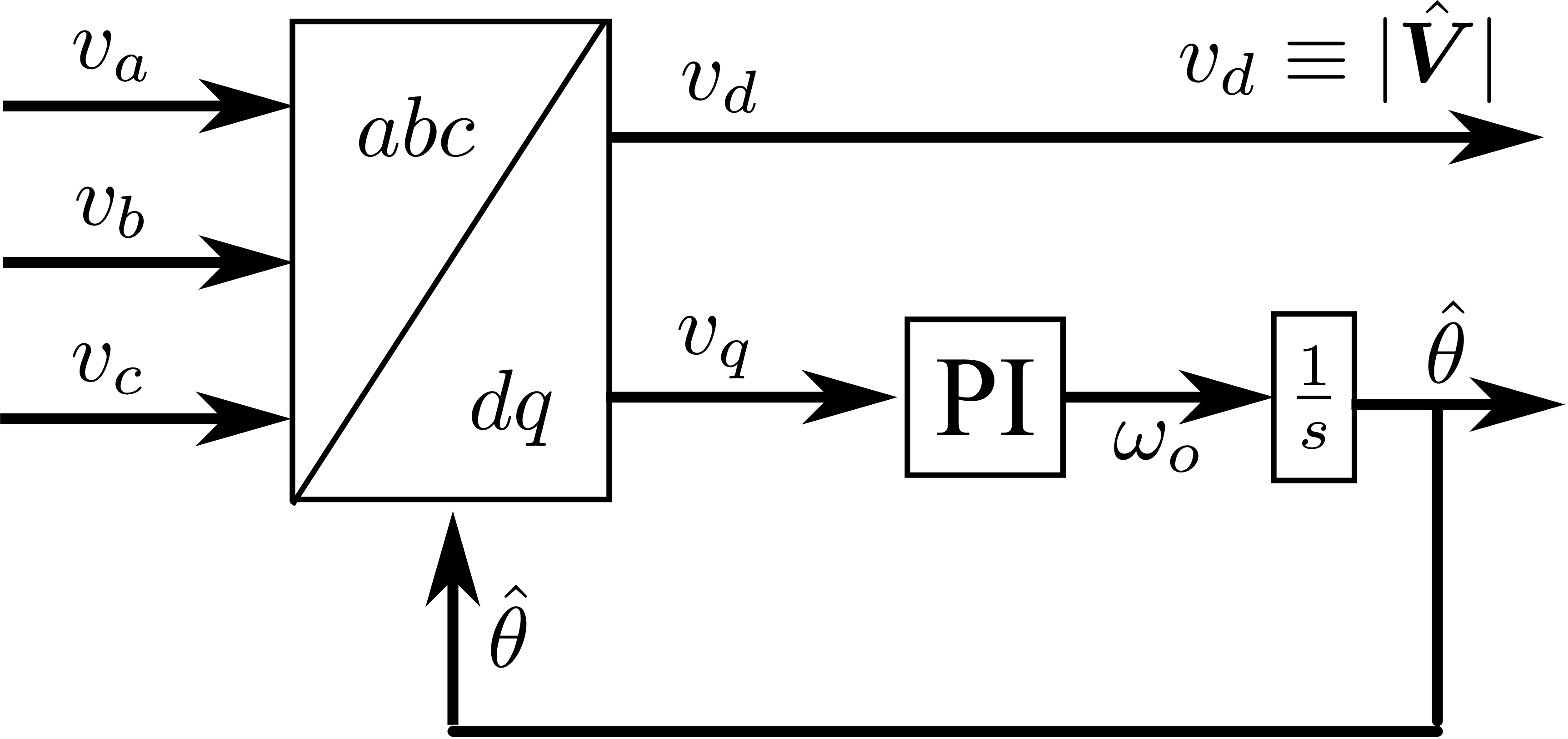
上面的锁相环控制框图有点复杂,可以简化简化。
简化版的三相锁相环控制框图,如图10所示。
经典三相锁相环有关数学公式
平衡的三相电网电压: \[ \begin{equation} \label{eq:BalancedThreePhaseVoltage} \begin{aligned} v_a &=\mathbf{V} \cos(\omega_1 t)\\ v_b &=\mathbf{V} \cos(\omega_1 t - 2\pi/3)\\ v_a &=\mathbf{V} \cos(\omega_1 t - 4\pi/3) \end{aligned} \end{equation} \]
\[ \begin{equation} \label{eq:AlphaBetaVoltage} \begin{aligned} \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} =\frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2}\\ \end{bmatrix} \begin{bmatrix} v_a\\ v_b\\ v_c \end{bmatrix} =\mathbf{V} \begin{bmatrix} \cos (\omega_1 t)\\ \sin (\omega_1 t) \end{bmatrix} =\mathbf{V} \begin{bmatrix} \cos \theta\\ \sin \theta \end{bmatrix} \end{aligned} \end{equation} \]
如果公式(26)中的三相平衡电压以 \(\sin\) 表示, \(abc\rightarrow \alpha\beta\) 的变换方程:
\[ \begin{equation} \begin{aligned} \label{eq:AlphaBetaVoltage2} \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} =\frac{2}{3} \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2}\\ \end{bmatrix} \begin{bmatrix} v_a\\ v_b\\ v_c \end{bmatrix} =\mathbf{V} \begin{bmatrix} \sin (\omega_1 t)\\ -\cos (\omega_1 t) \end{bmatrix} =\mathbf{V} \begin{bmatrix} \sin \theta\\ -\cos \theta \end{bmatrix} \end{aligned} \end{equation} \]
\[ \begin{equation} \begin{bmatrix} v_d\\ v_q \end{bmatrix} = \begin{bmatrix} \cos(\hat{\theta}) & \sin(\hat{\theta})\\ -\sin(\hat{\theta}) & \cos(\hat{\theta}) \end{bmatrix} \begin{bmatrix} v_\alpha\\ v_\beta \end{bmatrix} \end{equation} \]
\(\hat{\theta}=\omega_o t+\varphi_o\)
各物理量意义:
- \(\mathbf{V}\) 实际电压矢量
- \(\omega_1\) 电网电压角频率
- \(\theta\) 实际电压矢量的矢量角度
- \(\hat{\theta}\) 锁相环估计的电压矢量角度
- \(\omega_o\) 锁相环估计角频率
进一步简化计算: \[ \begin{equation} \label{eq:SimpleAlphaBetaToDQ} \begin{bmatrix} v_d\\ v_q \end{bmatrix} =\mathbf{V} \begin{bmatrix} \cos (\theta - \hat{\theta})\\ \sin (\theta - \hat{\theta}) \end{bmatrix} =\mathbf{V} \begin{bmatrix} \cos [(\omega_1 - \omega_o)t+\varphi_{error}]\\ \sin [(\omega_1 - \omega_o)t+\varphi_{error}] \end{bmatrix} \end{equation} \]
进行了一堆的数学推到过程,开始通过最后的数学表达式\(\eqref{eq:SimpleAlphaBetaToDQ}\)和图9开始分析三相锁相环原理。三相锁相环的鉴相器部分就是 \(v_q =\mathbf{V} \sin(\theta - \hat{\theta})\)。所以该控制结构实现了锁相环的鉴相器功能。
经典三相锁相环原理分析
输入信号和锁相环输出信号的可能性主要为频率和初相位的比较。频率不同\(\omega_1 \neq \omega_o\), \(v_q\) 是一个交流量。当频率锁定 \(\omega_1 = \omega_o\), \(v_q\) 是一个直流量。当频率和相位完全锁定, \(\omega_1=\omega_o,\varphi_{error}=0\),\(v_q=0\)。 而图9原理框图,因PI环节,正好能实现 \(v_q=0\) 要求。那么按照图9的原理便可实现锁相环的功能。
前面分析的三相锁相环的实现需要一个三相电网电压平衡的条件,对于不平衡的电网,无法适用。
不平衡电网电压对锁相环的影响
不平衡的电网电压可以用对称分量法分解成正序、负序和零序电压。
不平衡电网电压用正、负和零序电压表达式::
\[ \begin{equation} \label{eq:UnbalanceThreePhaseVoltage} \begin{aligned} v_a &=\mathbf{V}^+ \cos(\omega_1 t) + \mathbf{V}^- \cos(-\omega_1 t+\varphi^-) + \mathbf{V}^0 \cos(\omega_1 t + \varphi^0)\\ v_b &=\mathbf{V}^+ \cos(\omega_1 t - 2\pi/3) + \mathbf{V}^- \cos(-\omega_1 t - 2\pi/3+\varphi^-) + \mathbf{V}^0 \cos(\omega_1 t - 2\pi/3+\varphi^0)\\ v_a &=\mathbf{V}^+ \cos(\omega_1 t - 4\pi/3)+ \mathbf{V}^- \cos(-\omega_1 t - 4\pi/3+\varphi^-)+ \mathbf{V}^0 \cos(\omega_1 t - 4\pi/3+\varphi^0) \end{aligned} \end{equation} \]
\(0,+,-\) 分别代表零序,正序,负序。
\[ \begin{equation} \label{eq:PositiveAndNegativeComponentAlphaBeta} \mathbf{v}_{\alpha\beta}= \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} = \mathbf{V}^+ + \mathbf{V}^- =\mathbf{V}^+ \begin{bmatrix} \cos (\omega_1 t)\\ \sin (\omega_1 t) \end{bmatrix} +\mathbf{V}^- \begin{bmatrix} \cos (-\omega_1 t + \varphi^-)\\ \sin (-\omega_1 t + \varphi^-) \end{bmatrix} \end{equation} \]
通过公式\(~\eqref{eq:PositiveAndNegativeComponentAlphaBeta}\),可以得 到电网电压矢量的幅值和相位。
\[ \begin{equation} \label{eq:AmplitudeAndPhaseForUnbalance} \begin{aligned} |\mathbf{V}|=\sqrt{(\mathbf{V}^+)^2 + (\mathbf{V}^-)^2 + 2 \mathbf{V}^+ \mathbf{V}^- \cos(-2\omega t + \varphi^-)}\\ \theta = \omega t + \arctan(\frac{\mathbf{V}^- \sin (-2 \omega t + \varphi^-)} {\mathbf{V}^+ + \mathbf{V}^- \cos (-2\omega t + \varphi^{-1})}) \end{aligned} \end{equation} \]
由公式\(\eqref{eq:AmplitudeAndPhaseForUnbalance}\)可以知道,不平衡的电网电压会出现波动的幅值和相角(角频率)。而波动的幅值和相角对经典的三相锁相环有不利的影响。经典的三相锁相环适应理想的平衡三相电网电压,但对其他非理想情况需要额外的处理措施,来弥补其对非理想电网电压适应不足问题。
对应公式\(\eqref{eq:AmplitudeAndPhaseForUnbalance}\),可以提出使用低通滤波器滤波方案,来抑制不平衡电压中的谐波分量。但是引入滤波器会降低响应速度。 经典的三相锁相环适应理想的平衡三相电网电压,但对其他非理想情况需要额外的处理措施,来弥补其对非理想电网电压适应不足问题。
Se Kyo Chung 的三相锁相环闭环传递函数推导以及相角不平衡,谐波和直流偏置对三相锁相环误差理论分析写的不错3,值得一提的是该文献的实验结果图简单明了,值得一读。
为了用于不平衡的三相电网,也可以采取提取不平衡电网中正序电压电压。那么需要了解对称分量法的原理,以此来提取正序电压。
对称分量法
\(ABC\longrightarrow NP0\) 对于三相非平衡ABC(可以是电压,也可以是电流,甚至其他信号)可以分解成 \(N\)(negative sequence),\(P\)(positive sequence),\(0\)(zero sequence),这个方式被称为对称分量法。
\[ \begin{equation} \begin{bmatrix} P\\ N\\ 0 \end{bmatrix} = \frac{1}{3} \begin{bmatrix} 1 & \alpha & \alpha^2\\ 1 & \alpha^2 & \alpha\\ 1 & 1 & 1\\ \end{bmatrix} \begin{bmatrix} A\\ B\\ C\\ \end{bmatrix} \end{equation} \]
\[\alpha = e^{j\frac{2\pi}{3}}\]
\(NP0 \longrightarrow ABC\)
至于理论推到,用 \(NP0 \longrightarrow ABC\) 更易于理解。
\[ \begin{equation} \begin{bmatrix} A\\ B\\ C\\ \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1\\ \alpha^2 & \alpha & 1\\ \alpha & \alpha^2 & 1\\ \end{bmatrix} \begin{bmatrix} P\\ N\\ 0 \end{bmatrix} \end{equation} \]
提取的正序分量直接用于平衡三相锁相环的原理,便可解决三相锁相不平衡问题。但是该方法对变换频率的三相电网适应性差。提取正序分量用于锁相环的方法可参考文献4。
双同步坐标系解耦锁相环
针对三相电网不平衡的锁相问题,Rodriguez 等人提出了双同步坐标系解耦锁相环5,具有较高的响应速度、较高的鲁棒性和较精确的性能这一节的内容主要是理解双同步坐标系解耦锁相环原理。这一小节稍微有点复杂,不想看可以跳过,感兴趣或者闲来没事倒是可以看看。
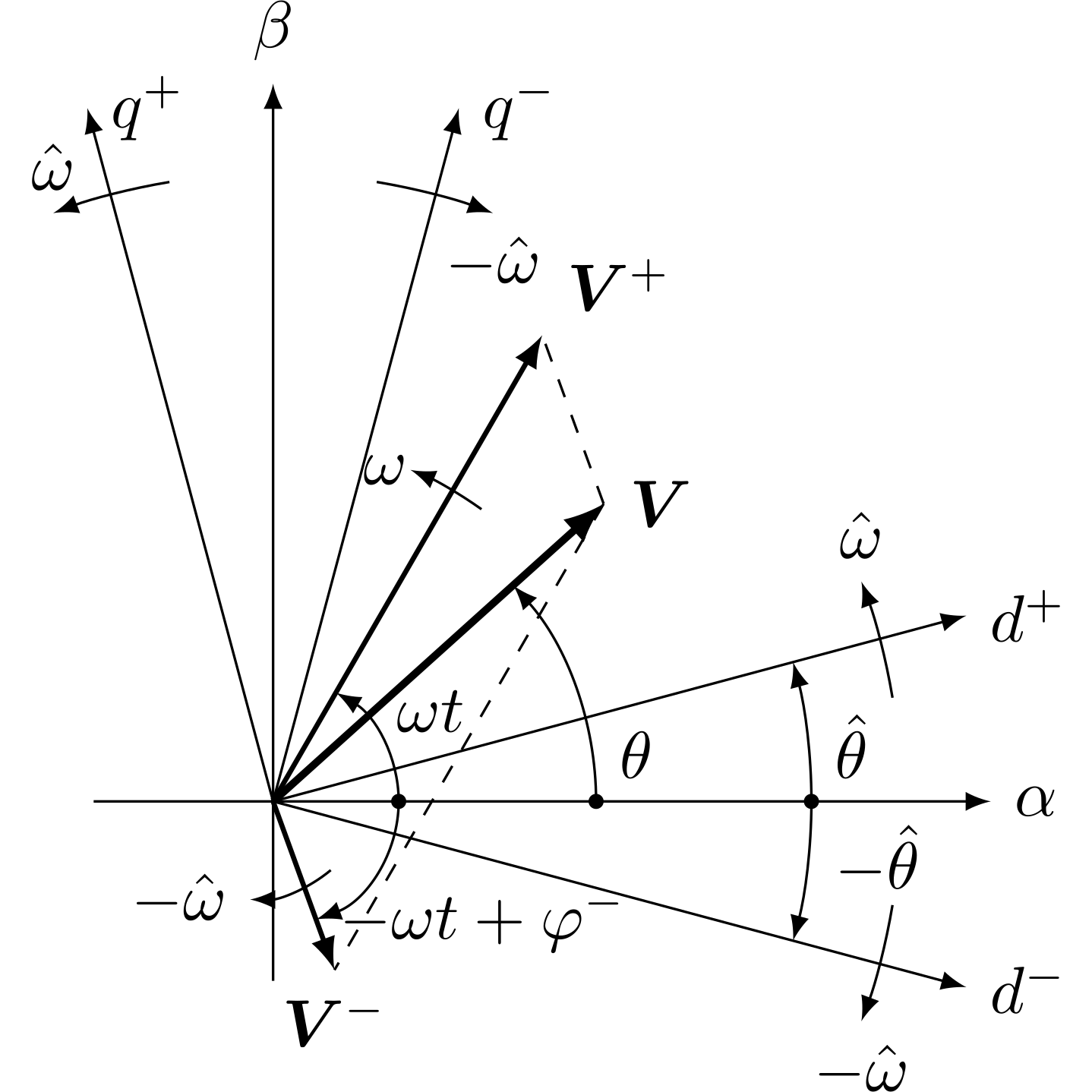
双同步坐标系故名思意该锁相环方法含有两个同步坐标系。
因此定义两个同步坐标系:
- \(dq^{+}\)坐标系,angular frequency: \(\hat{\omega}\),angluar position: \(\hat{\theta}\)
- \(dq^{-}\)坐标系,angular frequency: \(-\hat{\omega}\),angluar position: \(-\hat{\theta}\)
备注: 对于不平衡的三相电网电压系统,合成的电压矢量 \(\mathbf{V}\) 虽然频率是固定的,但是幅值是不断变化的。而当把三相不平衡电压使用对称分量法,可以分解成正序、负序和零序。因为中性点连接的系统,不存在零序分量。故只剩下正序和负序。同时单个负序或正序的电压矢量的幅值是恒定的。正、负序分别对应\(dq^+\)、\(dq^-\)同步坐标系。用\(dq^+\) 来锁相正序, \(dq^-\) 来锁相负序是没有问题。
定义的双坐标系和电压矢量如图11所示。
双同步坐标系的一些数学公式
conventional $ dq$ transformation matrix
\[ \begin{equation} \label{eq:AlphaBetaToDQ} \mathbf{T}_{dq}= \begin{bmatrix} \cos(\theta) & \sin(\theta)\\ -\sin(\theta) & \cos(\theta) \end{bmatrix} \end{equation} \]
从图11可以发现,\(dq^+\) 坐标系和我们传统的\(dq\)坐标系是一样的。故
\[ \begin{equation} \label{eq:AlphaBetaToDQPositive} \mathbf{T}_{dq^+}= \begin{bmatrix} \cos(\hat{\theta}) & \sin(\hat{\theta})\\ -\sin(\hat{\theta}) & \cos(\hat{\theta}) \end{bmatrix} \end{equation} \]
而\(dq^-\)坐标系的位置角为 \(-\hat{\theta}\), 故
\[ \begin{equation} \label{eq:AlphaBetaToDQNegative} [\mathbf{T}_{dq^-}]= \begin{bmatrix} \cos(-\hat{\theta}) & \sin(-\hat{\theta})\\ -\sin(-\hat{\theta}) & \cos(-\hat{\theta}) \end{bmatrix} = \begin{bmatrix} \cos(\hat{\theta}) & -\sin(\hat{\theta})\\ \sin(\hat{\theta}) & \cos(\hat{\theta}) \end{bmatrix} =[\mathbf{T}_{dq^+}]^T \end{equation} \]
根据公式 \(\eqref{eq:PositiveAndNegativeComponentAlphaBeta}\),再结合 \(\mathbf{T}_{dq^+}\) 和 \(\mathbf{T}_{dq^-}\),可以获得 \(\mathbf{v}_{dq^+}\) 和 \(\mathbf{v}_{dq^+}\):
\[ \begin{equation} \label{eq:DoubelSychrounousDQ} \begin{aligned} \mathbf{v}_{dq^+}= \begin{bmatrix} v_{d^+}\\ v_{q^+} \end{bmatrix} =[\mathbf{T}_{dq^+}] \mathbf{v}_{\alpha\beta} =\mathbf{V}^+ \begin{bmatrix} \cos (\omega t -\hat{\theta})\\ \sin (\omega t -\hat{\theta}) \end{bmatrix} +\mathbf{V}^- \begin{bmatrix} \cos (-\omega t + \varphi^- - \hat{\theta})\\ \sin (-\omega t + \varphi^- - \hat{\theta}) \end{bmatrix}\\ \mathbf{v}_{dq^-}= \begin{bmatrix} v_{d^-}\\ v_{q^-} \end{bmatrix} =[\mathbf{T}_{dq^-}] \mathbf{v}_{\alpha\beta} =\mathbf{V}^+ \begin{bmatrix} \cos (\omega t +\hat{\theta})\\ \sin (\omega t +\hat{\theta}) \end{bmatrix} +\mathbf{V}^- \begin{bmatrix} \cos (-\omega t + \varphi^- + \hat{\theta})\\ \sin (-\omega t + \varphi^- + \hat{\theta}) \end{bmatrix} \end{aligned} \end{equation} \]
前面我们已经知道,使用单同步坐标系的锁相环控制结构是可以实现 \(\hat{\theta} \approx \omega t\),那么对于双同步坐标系,各自独立闭环运行,依旧可以实现 \(\hat{\theta} \approx \omega t\)。那么 \(\hat{\theta} - \omega t\) 为一个很小的值,可以采用小信号分析方法。有如下的近似等式:
\[ \begin{equation} \label{eq:sincosapprox} \begin{aligned} \sin(\omega t - \hat{\theta}) & \approx \omega t - \hat{\theta}\\ \cos(\omega t - \hat{\theta}) & \approx 1 - ((\omega t - \hat{\theta})^2/2)\\ -\omega t - \hat{\theta} & \approx -2 \omega t \end{aligned} \end{equation} \]
根据公式\(\eqref{eq:sincosapprox}\),可以化简公式\(\eqref{eq:DoubelSychrounousDQ}\),得到一个简化版结果。
\[ \begin{equation} \label{eq:SimpleDoubelSychrounousDQ} \begin{aligned} \mathbf{v}_{dq^+} &=\mathbf{V}^+ \begin{bmatrix} 1 - (\omega t -\hat{\theta})^2/2\\ \omega t -\hat{\theta} \end{bmatrix} +\mathbf{V}^- \begin{bmatrix} \cos (-2\omega t + \varphi^-)\\ \sin (-2\omega t + \varphi^-) \end{bmatrix}\\ \mathbf{v}_{dq^-} &=\mathbf{V}^+ \begin{bmatrix} \cos (2\omega t)\\ \sin (2\omega t) \end{bmatrix} +\mathbf{V}^- \begin{bmatrix} \cos (\varphi^-)\\ \sin (\varphi^-) \end{bmatrix} \end{aligned} \end{equation} \]
至于得到简化的公式有何意义?\(dq^+\) 和 \(dq^-\) 坐标系的直流分量与电网电压的正序和负序分量的幅值有关,而2次谐波分量是分解两同步旋转坐标系而造成的耦合分量。接下来主要目标就是解耦耦合分量,或者说消除耦合分量。
解耦网络
为进行一般化分析,假设任意电压矢量包括正、负序分量两部分,分别以角速度 \(n\omega\) 和 \(m\omega\) 旋转,其中 \(n\) 、\(m\) 分别表示正、负序。电网角频率\(\omega\)。通过公式\(\eqref{eq:PositiveAndNegativeComponentAlphaBeta}\),可以得电压矢量的正、负序分量表示为:
\[ \begin{equation} \label{eq:GeneralPositiveAndNegativeComponentAlphaBeta} \mathbf{v}_{\alpha\beta}= \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} = \mathbf{V}_{\alpha\beta}^n + \mathbf{V}_{\alpha\beta}^m =\mathbf{V}^{n} \begin{bmatrix} \cos (n \omega t + \varphi^n)\\ \sin (n \omega t + \varphi^n) \end{bmatrix} +\mathbf{V}^{m} \begin{bmatrix} \cos (m \omega t + \varphi^m)\\ \sin (m \omega t + \varphi^m) \end{bmatrix} \end{equation} \]
\(\varphi^n\) 和 \(\varphi^m\) 正序和负序电压矢量的初始相位角。
现在正序、负序两个旋转坐标系分别用 \(dq^n\) 和 \(dq^m\) 来表示。\(n \hat{\theta}\) 和\(m \hat{\theta}\) 则表示正、负序的两个旋转坐标系的相位角度。\(\hat{\theta}\) 为锁相环输出角度。
先假设锁相环能完全锁相,即有 \(\hat{\theta}=\omega t\)。(至于为什么要这样假设?在理想的锁相的条件下,找出影响波动的原因,并把波动量消除,便可得到正确的锁相。同时,在常规的三相锁相环结构,就可以达到\(\hat{\theta} \approx \omega t\)的效果,因此做这样的假设是合理的操作)。那么,公式\(\eqref{eq:GeneralPositiveAndNegativeComponentAlphaBeta}\) 在 \(dq^n\) 和 \(dq^m\) 坐标系下表达式为:
\[ \begin{equation} \label{eq:MNDoubelSychrounousDQ} \begin{aligned} \mathbf{v}_{dq^n} &= \begin{bmatrix} v_{d^n}\\ v_{q^n} \end{bmatrix} =[\mathbf{T}_{dq^n}] \mathbf{v}_{\alpha\beta}= \begin{bmatrix} \cos(n\hat{\theta}) & \sin(n\hat{\theta})\\ -\sin(n\hat{\theta}) & \cos(n\hat{\theta}) \end{bmatrix} \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} \\ &= \mathbf{V}^n \begin{bmatrix} \cos (\varphi^n)\\ \sin (\varphi^n) \end{bmatrix} +\mathbf{V}^m\cos(\varphi^m) \begin{bmatrix} \cos ((n-m)\omega t)\\ -\sin( (n-m)\omega t) \end{bmatrix} +\mathbf{V}^m\sin(\varphi^m) \begin{bmatrix} \sin ((n-m)\omega t)\\ \cos ((n-m)\omega t) \end{bmatrix}\\ \mathbf{v}_{dq^m} &= \begin{bmatrix} v_{d^m}\\ v_{q^m} \end{bmatrix} =[\mathbf{T}_{dq^m}] \mathbf{v}_{\alpha\beta}= \begin{bmatrix} \cos(m\hat{\theta}) & \sin(m\hat{\theta})\\ -\sin(m\hat{\theta}) & \cos(m\hat{\theta}) \end{bmatrix} \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} \\ &=\mathbf{V}^m \begin{bmatrix} \cos \varphi^m\\ \sin \varphi^m \end{bmatrix} +\mathbf{V}^n\cos(\varphi^n) \begin{bmatrix} \cos ((n-m)\omega t)\\ \sin ((n-m)\omega t) \end{bmatrix} +\mathbf{V}^n\sin(\varphi^n) \begin{bmatrix} -\sin ((n-m)\omega t)\\ \cos ((n-m)\omega t) \end{bmatrix}\\ \end{aligned} \end{equation} \]
从公式\(\eqref{eq:MNDoubelSychrounousDQ}\),我们得到了在锁相状态(\(\omega t = \hat{\theta}\))下的 \(\mathbf{v}_{dq^n}\)和\(\mathbf{v}_{dq^n}\)的表达式。通过表达式可以知道,\(dq^n\)坐标系下的交流量(振荡量)的幅值由 \(dq^m\) 坐标系下的平均值所决定。与之对应的, \(dq^m\) 坐标系下的交流量的幅值由\(dq^n\)坐标系下的平均值决定。解耦的目标就是消除振荡量(交流量)。既然实际的\(\mathbf{v}_{dq^n}\) 和 \(\mathbf{v}_{dq^m}\) 中含有交流量部分,为了消除交流量,可以,便可消除交流部分。 以消除交流分量为目标,如图12所示,为\(dq^n\) 坐标系下的解耦网络。
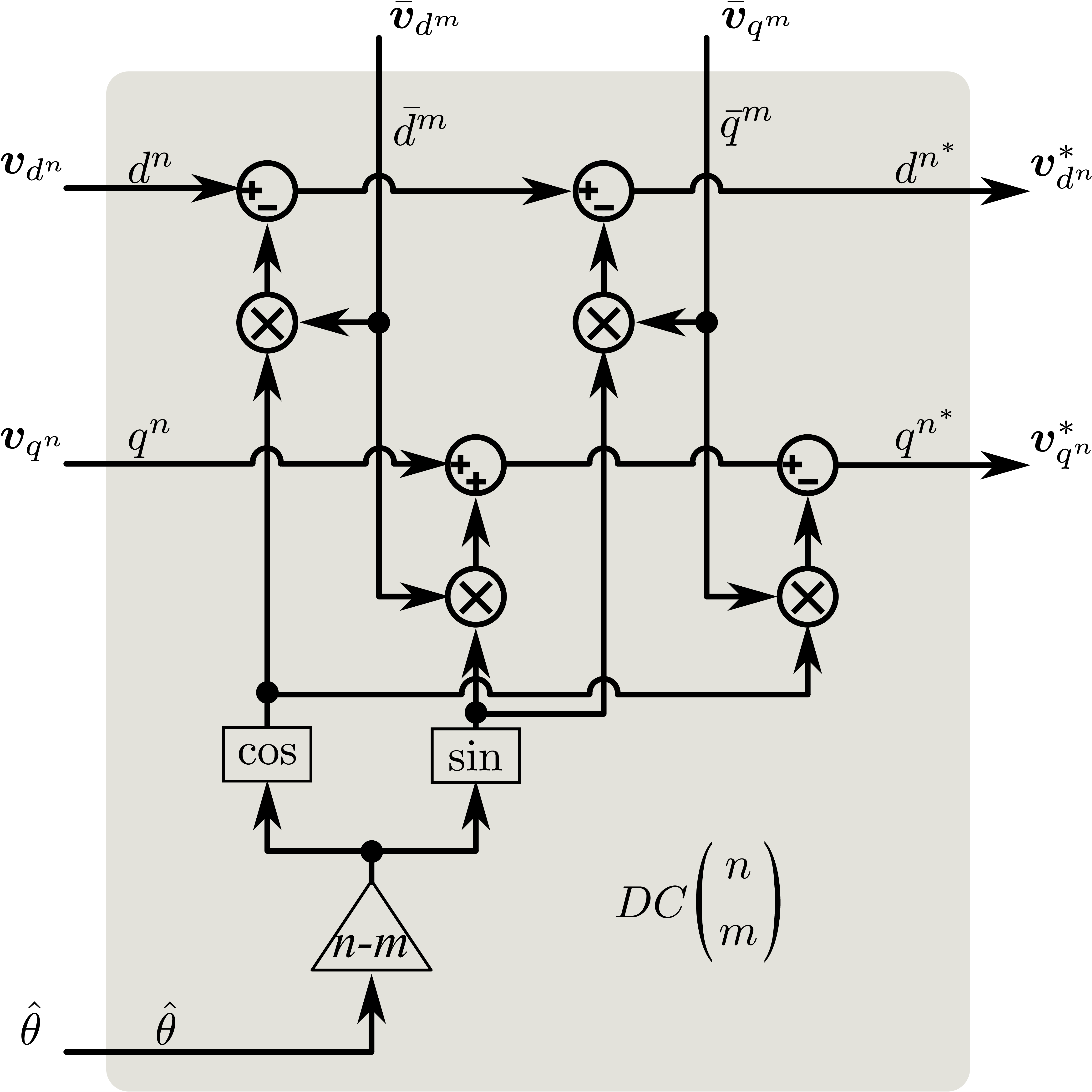
针对\(dq^m\)坐标系,可以根据公式\(\eqref{eq:MNDoubelSychrounousDQ}\),构造对应的解耦网络。
那么\(dq^n\)和\(dq^m\)双同步坐标系的解耦网络如图13所示。其中LPF是一个一阶低通滤波器,其传递函数可表示为:
\[ \begin{equation} LPF(s)=\frac{\omega_f}{s+\omega_f} \end{equation} \]
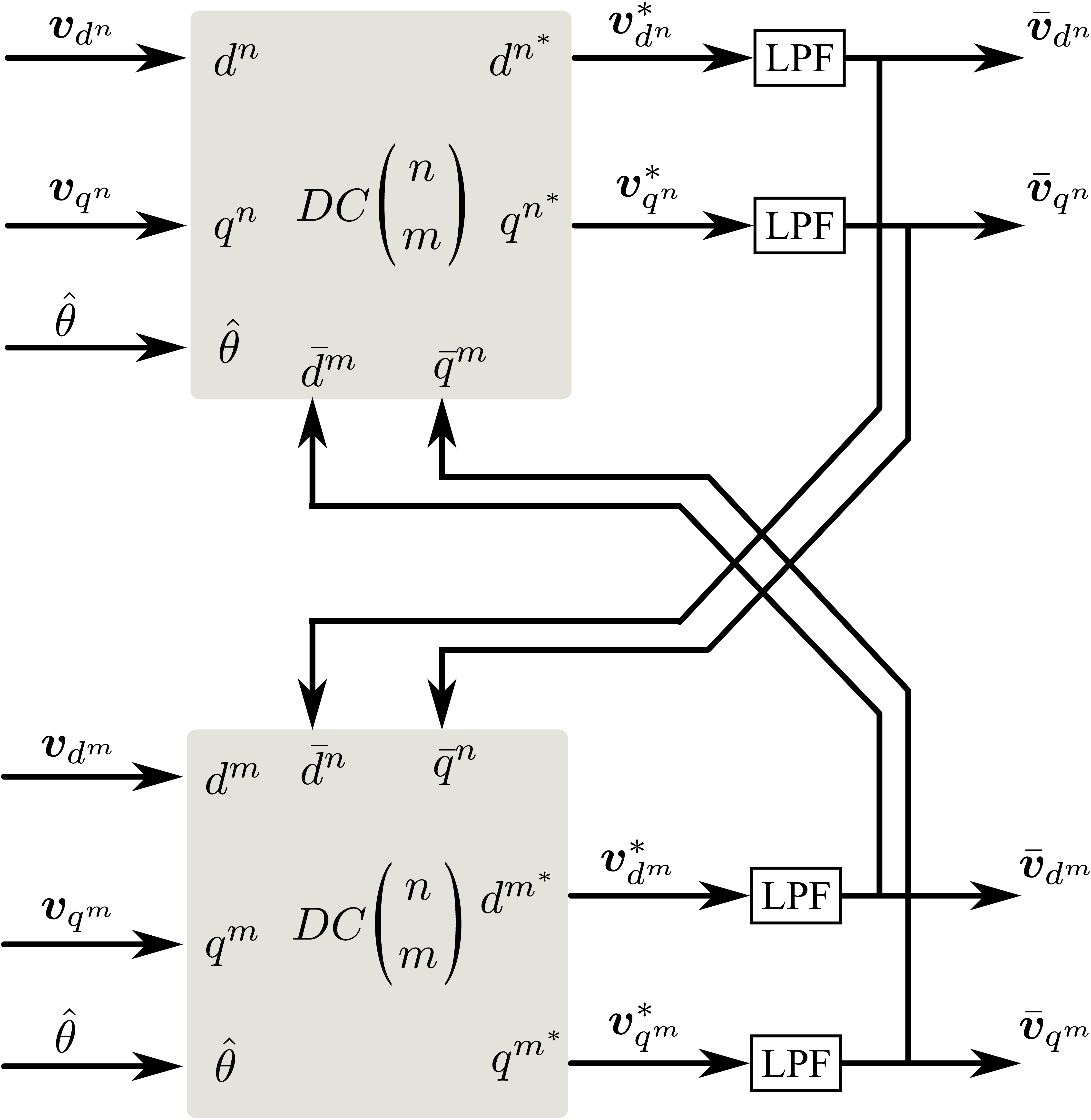
文献[5]中,在这个解耦网络的基础上,进一步用状态空间方程来表示该解耦网络。个人认为,对于理解双坐标系的锁相环原理到此,就可以完全理解其核心理念了。文献[5]用状态空间模型的目的大概在于表达形式更统一,简便吧!
通过对解耦网络图13和传统的三相锁相环结构图10整合,可以得到双同步坐标系下锁相环整个原理框图,如图14所示。 \(n\) 或 \(m\) 分别代表正负序的意义。
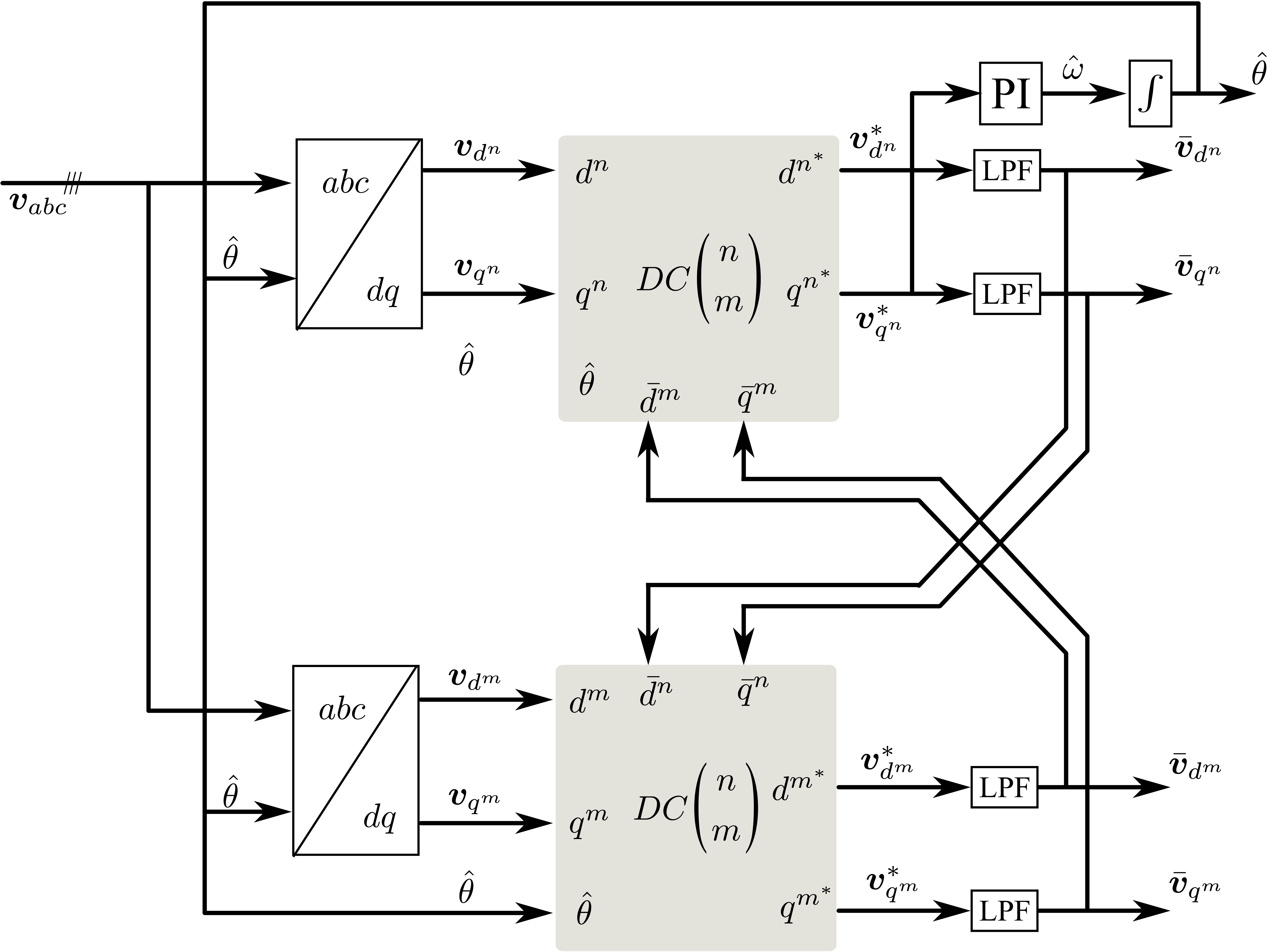
该方法解决了前面提取正序方案无法应对变换频率的问题。对频率具有良好的适应性。尽管该接偶环节加了一个一阶低通滤波器降低了响应速度,但是该锁相环的效果还是不错的。三相锁相环的研究就告一段落。接下来开始研究单相锁相环。
虚拟平均无功鉴相单相锁相环
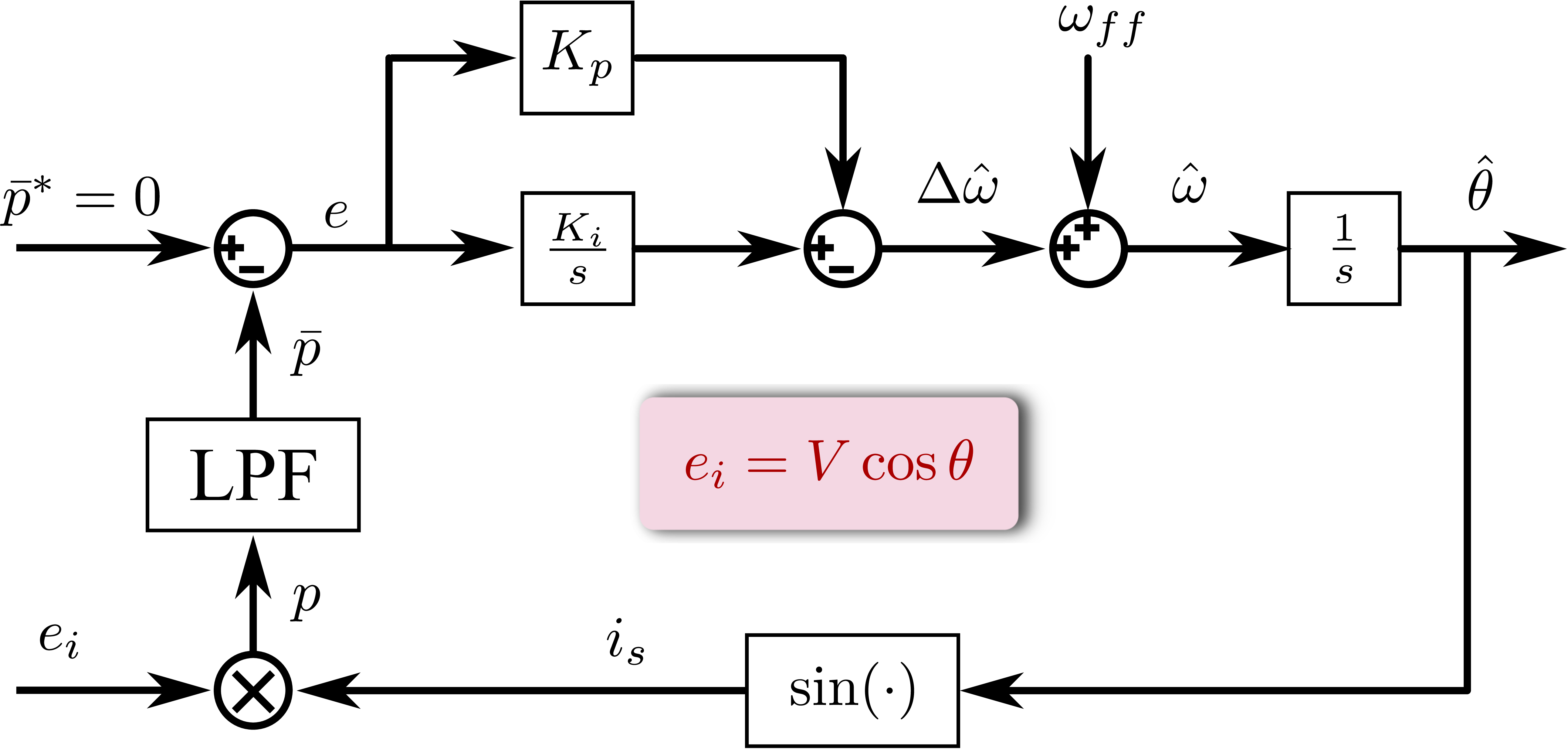
该方法取了一个高大上的名字虚拟平均无功鉴相单相锁相环,实际从本质上来看就是最开始分析的乘法鉴相锁相环。如果再本质一点就是乘法器。
输入信号:
\[ \begin{equation} e_i=V\cos \theta \end{equation} \]
锁相环输出相角:\(\hat{\theta}\)
定义一个虚拟的电流\(i_s\)(简单的说就是一个假想的物理量,在真实的物理世界不存在的物理量)重要的是它的数学表达式:
\[ \begin{equation} i_s=\sin \hat{\theta} \end{equation} \]
上面\(e_i\)和 \(i_s\) 经过乘法器得到的结果,定义为虚拟无功功率\(p\):
\[ \begin{equation} p=V\cos\theta \sin \hat{\theta} \end{equation} \]
三角函数积化和差公式用于 \(p\):
\[ \begin{equation} p=\frac{V}{2}\sin (\hat{\theta} - \theta) +\frac{V}{2} \sin (\hat{\theta} + \theta) \end{equation} \]
和乘法器鉴相锁相环相似的处理逻辑,低通滤波器滤除\(\frac{V}{2} \sin (\hat{\theta} + \theta)\) 交流分量,得到无功功率平均值\(\bar{p}\)。
\[ \begin{equation} \bar{p}=\frac{V}{2}\sin (\hat{\theta} - \theta) \end{equation} \]
假设该系统成功锁相,那么有 \(\theta \approx \hat{\theta}\), 小信号处理,可以得到
\[ \begin{equation} \bar{p} = \frac{V}{2}(\hat{\theta} - \theta) \end{equation} \]
那么只要控制\(\bar{p}\)为0,便可以实现锁相。这也是 \(\bar{p}^{ * }=0\) 的原因。
虚拟平均无功鉴相单相锁相环的整个原理,控制结构图15充分展现其原理。
该方法简单,但该方法的动态性能比较弱(添加了低通滤波器LPF)。它对电网谐波不敏感,算一个优点吧。无法获得电网的幅值信息,算一个缺点吧。
增强型单相锁相环EPLL
为了解决虚拟平均无功鉴相单相锁相环动态响应速度慢的问题,采用基于自适应滤波理论的来重构输入信号的基波分量,同时可以实现对输入信号幅值、相位角与频率的估算。把这种基于自适应滤波理论的锁相环称为增强型单相锁相环6.
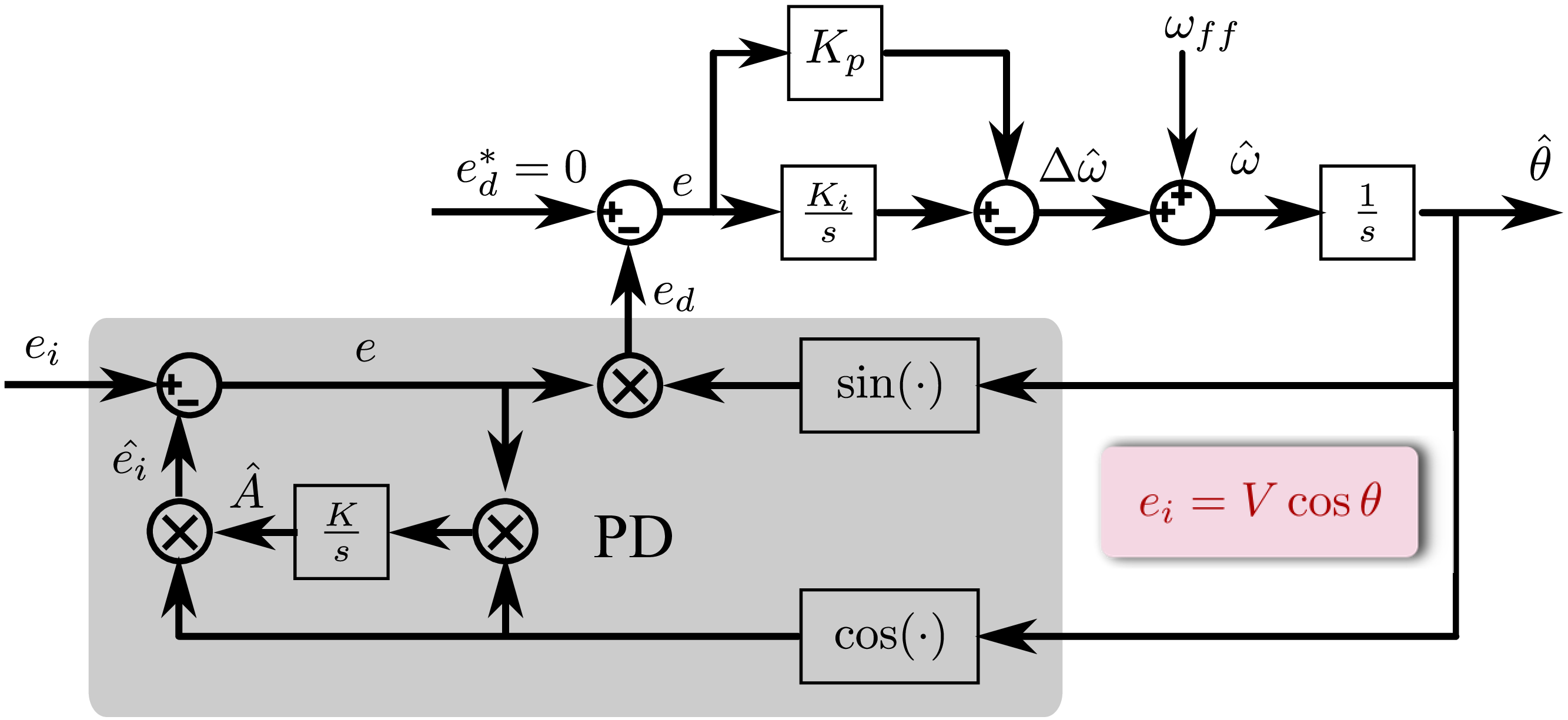
该控制结构多了一个比较陌生的变量\(\hat{A}\),他是用来估算输入锁相信号的幅值。
根据图16的控制结构,可以写出\(e_d\)
\[ \begin{equation} \label{eq:SingleEpllPDSignal} \begin{aligned} e_d &= e \times \sin \hat{\theta}\\ &= (e_i-\hat{e_i}) \sin \hat{\theta}\\ &= (\hat{A} \cos \hat{\theta}-V\cos \theta) \sin \hat{\theta}\\ &= \frac{V}{2} \sin (\hat{\theta} -\theta)+ \frac{V}{2} \sin (\theta + \hat{\theta}) - \frac{\hat{A}}{2} \sin 2 \hat{\theta} \end{aligned} \end{equation} \]
仔细端详该控制结构框图,会发现在稳态时,有\(\hat{A} \approx V\), \(\hat{\theta} \approx \theta\),在使用小信号模型分析方法,可以简化公式\(\eqref{eq:SingleEpllPDSignal}\),得到一个有关相位差的公式。
\[ \begin{equation} e_d = \frac{V}{2} (\hat{\theta}-\theta) \end{equation} \]
值得注意的是控制框图中的PD环节中有一个积分系数 \(K\), \(K\)的大小决定的是线电压幅值估算值 \(\hat{A}\) 的收敛速度。\(\hat{A}\)的收敛目标就是线电压幅值。
该锁相环的近似闭环传递函数:
\[ \begin{equation} H(s)=K_v \frac{s K_p + K_i}{s^2+s K_v K_p + K_v K_i} \end{equation} \]
\(K_v\) 为鉴相器的稳态增益, \(K_v=\frac{V}{2}\)。但是该闭环传递函数如何得来的,目前还不是特别清楚?
该方案替换了低通滤波器,通过使\(\frac{V}{2} \sin (\theta + \hat{\theta})\)、\(\frac{\hat{A}}{2} \sin 2 \hat{\theta}\) 两者抵消的方案实现交流量的滤除。尽管提高了锁相环的响应速度,具有较好的动态性能。但是该锁相环方案对谐波比较敏感。不适合含有大量谐波的场合,需要先进行谐波滤除,才能应用该方案。
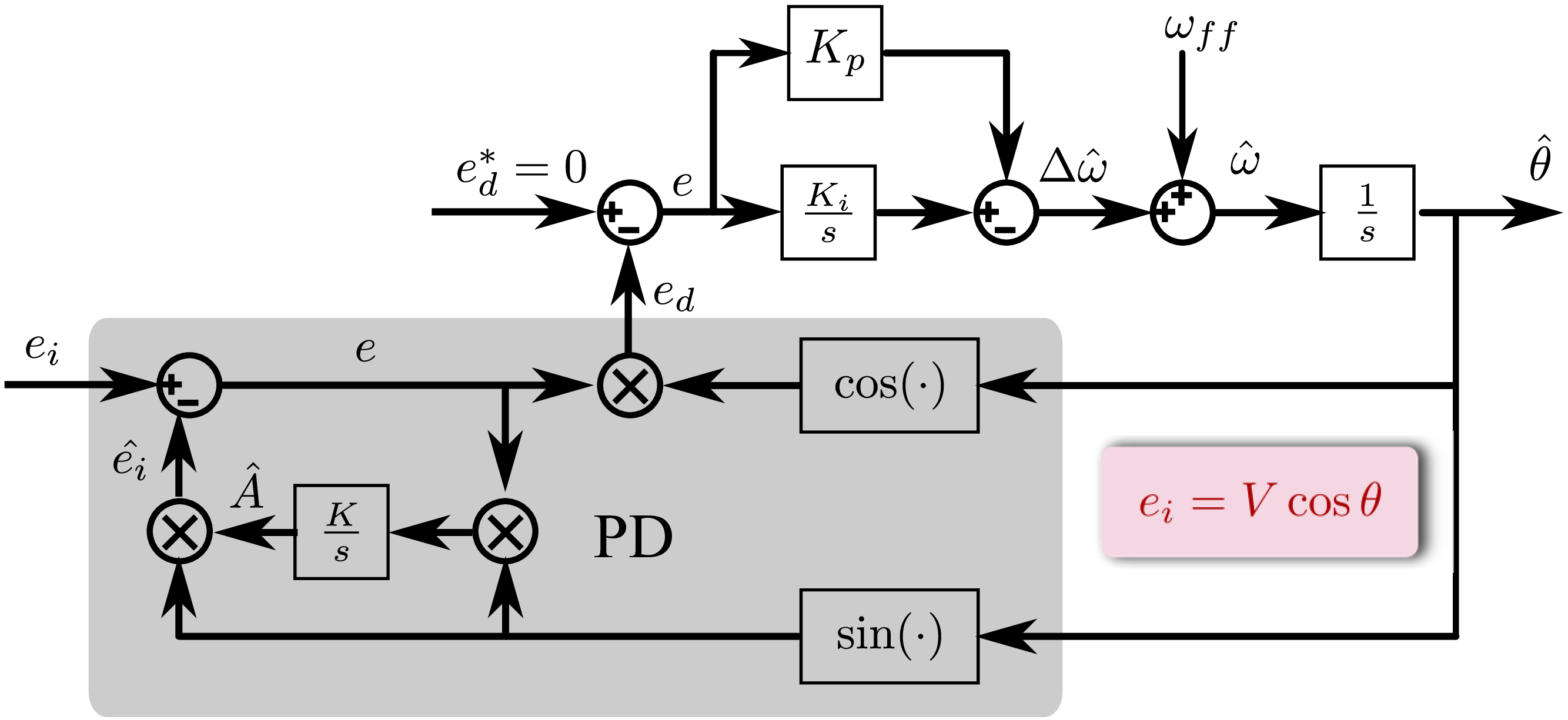
图16的控制结构和图17只是\(\sin\)和\(\cos\)互换,依然能实现锁相环的功能。
基于延迟法的虚拟两相的单相锁相环
前面针对单相锁相环的处理都是集中在单个输入信号。当然,可以采取前面的三相锁相环的思路,来构造一个虚拟的正交信号,来模仿三相锁相环的原理。输入信号定义为\(v_{\beta}\),经过\(90^{\circ}\)的延时来虚拟一个\(v_{\alpha}\)。而通过公式\(\eqref{eq:AlphaBetaVoltage}\)可以知道,\(v_{\alpha}\) 的相角和三相的\(v_a\)相角对应(这句话实际没啥意义,可以忽略!)。有了\(v_{\alpha}\)和 \(v_{\beta}\),那么就可以使用三相锁相环的处理方案。
如图18所示,为基于延迟法的虚拟两相的单相锁相环的控制结构。和经典的三相锁相环结构对比对比就可以理解啦!延迟\(90^{\circ}\)的方法,影响响应速度。
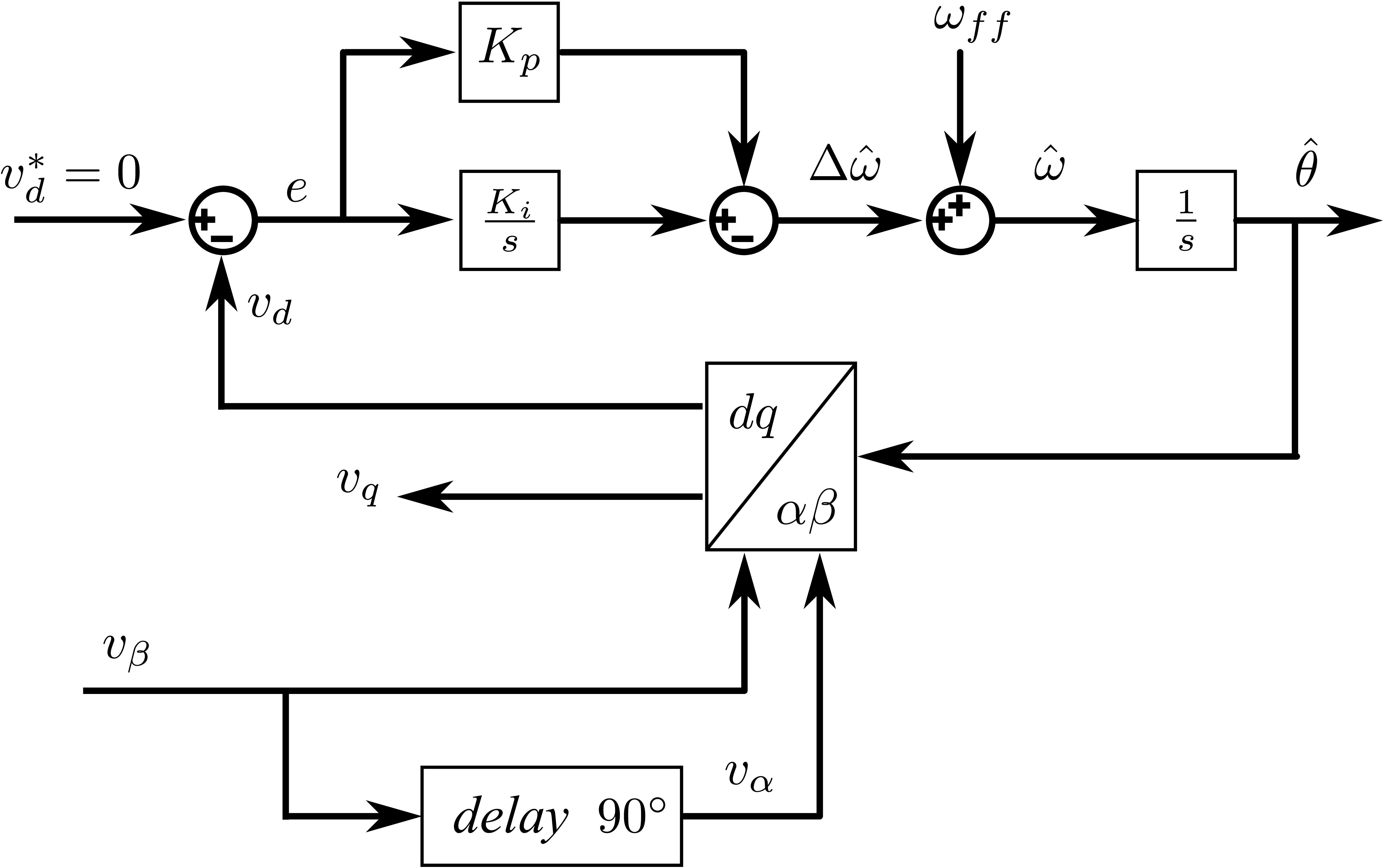
基于微分法的虚拟两相的单相锁相环
知道\(v_{\beta}\) 获得 \(v_{\alpha}\) 的方式,除了使用延迟方式,还可以使用微分的方式。但是有个一个前提, 输入信号\(v_{\beta}\)为理想的正弦信号。对于非理想电网就会出现问题。尽管速度提高了,但微分环节的引入,抗噪声能力严重下降。
如果想把非理想正弦的信号变换为正弦的理想信号,又需要加入滤波器,这又引入了延迟。哈哈!进入无限死循环。该微分法的原理框图不在列出,本质上和基于延迟法的单相锁相环没有差别。
基于Park反变换虚拟两相的单相锁相环
基于Park反变换的方法有点意思,所以把控制结构图列出来,如图19所示。尽管文献7有其他分析思路,但是我更倾向于更简单有效的理解方式。把这个反Park变换作为估计\(v_{\beta}\)的一种观测器来理解。同样和前面的基于虚拟两相的方法具有一曲同功之妙。已知输入信号\(v_{\alpha}\),通过坐标变换获得\(v_{\beta}\),然后使 \(v_d=0\),即可实现锁相环功能。
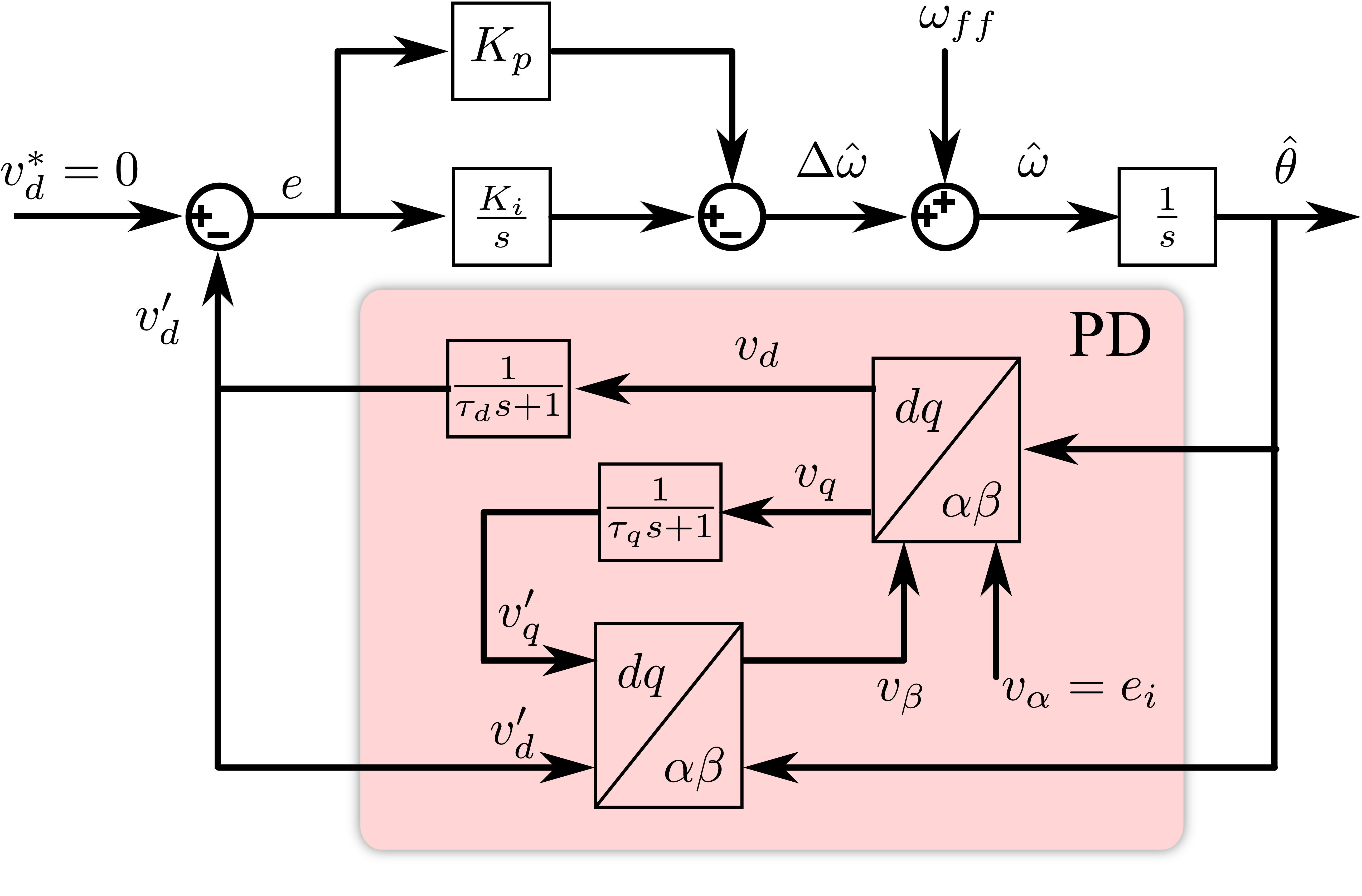
列写几个变换方程(通过上面结构框图可以得到),意思意思一下。
\[ \begin{equation} \begin{bmatrix} v_d\\ v_q \end{bmatrix} = \begin{bmatrix} \cos(\hat{\theta}) & \sin(\hat{\theta})\\ -\sin(\hat{\theta}) & \cos(\hat{\theta}) \end{bmatrix} \begin{bmatrix} v_{\alpha}\\ v_{\beta} \end{bmatrix} \end{equation} \]
\[ \begin{equation} \begin{bmatrix} v_{\alpha}'\\ v_{\beta}' \end{bmatrix} = \begin{bmatrix} \cos(\hat{\theta}) & -\sin(\hat{\theta})\\ \sin(\hat{\theta}) & \cos(\hat{\theta}) \end{bmatrix} \begin{bmatrix} v_d'\\ v_q' \end{bmatrix} \end{equation} \]
\[v_{\beta}=v_{\beta}'\]
\[ \begin{equation} v_{d}'(s)=\frac{v_d(s)}{\tau_d s + 1} \end{equation} \]
\[ \begin{equation} v_{q}'(s)=\frac{v_q(s)}{\tau_d s + 1} \end{equation} \]
基于SOGI的单相锁相环
SOGI全称为 Second-Order Generalized Integrator,翻译成中文为二阶广义积分器。基于SOGI的单相锁相环的核心就是SOGI,如果明白SOGI,剩下的问题就迎刃而解啦!
简单的说一下SOGI的功能:SOGI的两个输出信号严格的满足\(90^{\circ}\)的相位偏差(两输出信号严格的正交),同时其中一个输出能精确的跟踪输入基频信号。
如果能得到两个严格正交的信号,可以分别定义为\(v_{\alpha}\)、\(v_{\beta}\),那么再利用前面经典的三相锁相环原理,便可实现锁相环功能。
如图20所示,为SOGI-QSG(Second-Order Generalized Integrator Quadrature Signals Generation)的原理框图。
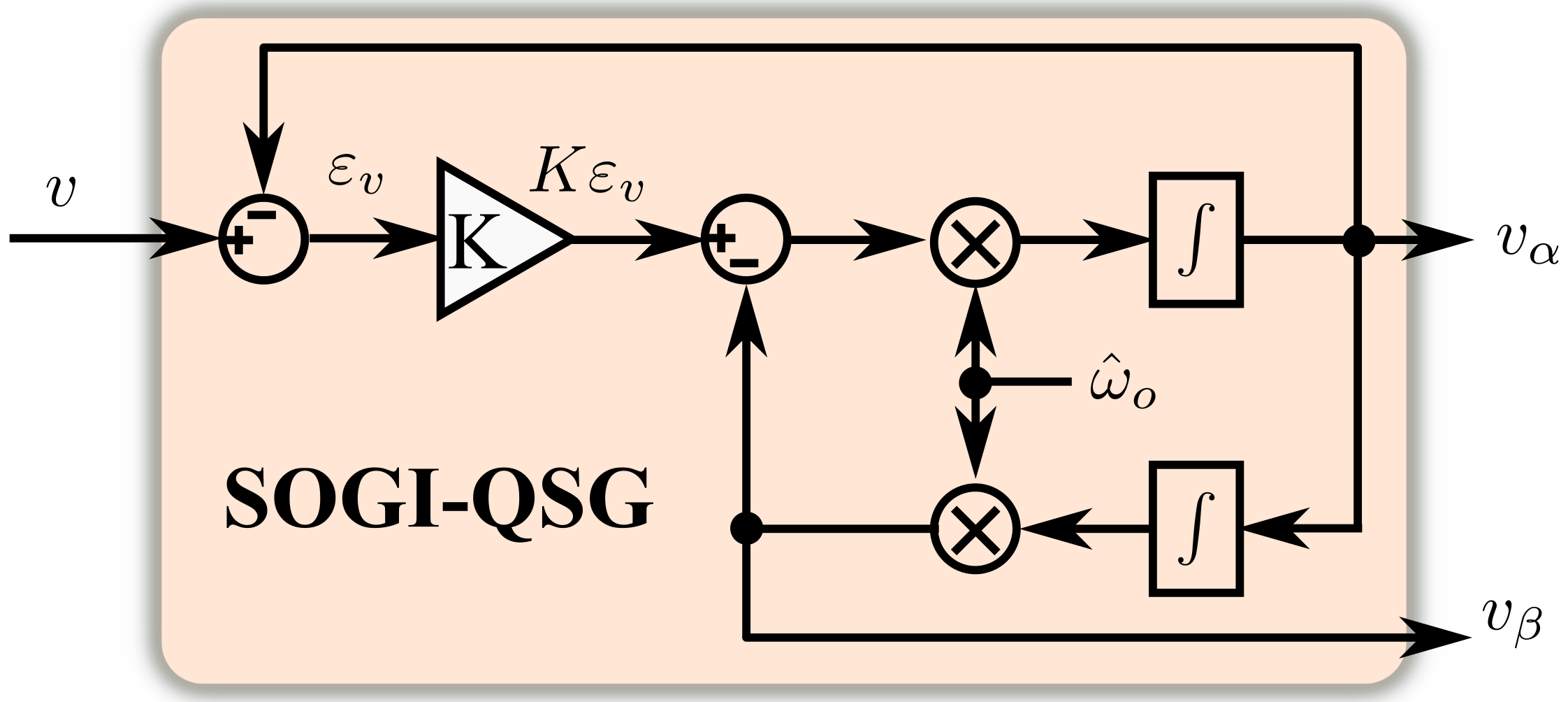
为什么SOGI能精确跟踪为正弦的输入信号?
根据图20,可以得到SOGI的开环传递函数:
\[ \begin{equation} \label{eq:SOGIOpenLoopTransferFunction} \begin{aligned} \frac{v_{\alpha}(s)}{K\varepsilon_v(s)} &=\frac{s \hat{\omega_o}}{s^2+\hat{\omega_o}^2}\\ \frac{v_{\beta}(s)}{K\varepsilon_v(s)} &=\frac{\hat{\omega_o}^2}{s^2+\hat{\omega_o}^2} \end{aligned} \end{equation} \]
正弦信号的 laplace 变换
\[ \begin{equation} \label{eq:SinusoidalLaplaceTransfer} \begin{aligned} \mathcal{L}\{\sin(\omega t)\}&=\frac{\omega}{s^2+\omega^2}\\ \mathcal{L}\{\cos(\omega t)\}&=\frac{s}{s^2+\omega^2} \end{aligned} \end{equation} \]
根据内膜原理8,可以用一句简单的话来说,整个控制系统要使输入信号与输出信号无静差,完全精准跟踪输入信号,那么只要满足控制系统的开环传递函数中含有输入信号的s域模型的条件,便可实现精准无静差跟踪。
比较好的 The Internal Model Principle 教程是 Purdue 大学 Zak 教授的这一篇内膜原理笔记。有兴趣,可以读一读。
观察公式 \(\eqref{eq:SOGIOpenLoopTransferFunction}\)和公式\(\eqref{eq:SinusoidalLaplaceTransfer}\)你会发现恰巧SOGI的开环传递函数含有正弦信号的s域模型。那么就解决了为什么SOGI可以精确跟踪正弦信号。
为什么SOGI两输出信号严格正交?
SOGI的闭环传递函数: \[ \begin{equation} \label{eq:SOGIClosedLoopTransferFunction} \begin{aligned} G_{\alpha} &=\frac{v_{\alpha}(s)}{v(s)} =\frac{ks}{s^2+ks+\hat{\omega_o}^2}\\ G_{\beta} &=\frac{v_{\beta}(s)}{v(s)} =\frac{k\hat{\omega_o}}{s^2+ks+\hat{\omega_o}^2} \end{aligned} \end{equation} \]
可以直接看两闭环传递函数\(\eqref{eq:SOGIClosedLoopTransferFunction}\)互差\(90^{\circ}\)。
\[ \begin{equation} \angle G_{\alpha} - \angle G_{\beta}=\frac{\pi}{2} \end{equation} \]
因此SOGI的两输出信号严格正交。
从闭环传递函数 Bode 图中也可以验证SOGI输出信号严格正交, \(G_{\alpha}\)、 \(G_{\beta}\) 相角严格互差\(\frac{\pi}{2}\)。
从图21可以发现,\(G_{\alpha}\)可以看作一个带通滤波器,在频率 \(\hat{\omega_o}\) 处无衰减,但在其它频率就有衰减作用,越偏离 \(\hat{\omega_o}\),衰减越厉害。这也是锁相环所期望的,锁定频率基本不衰减,其他次谐波都衰减,过滤。因此基于SOGI的单相锁相环性能不错,能抵抗谐波干扰。
写了这么多理论,放一个基于 SOGI 的 simulink 的仿真波形吧!如图22所示。
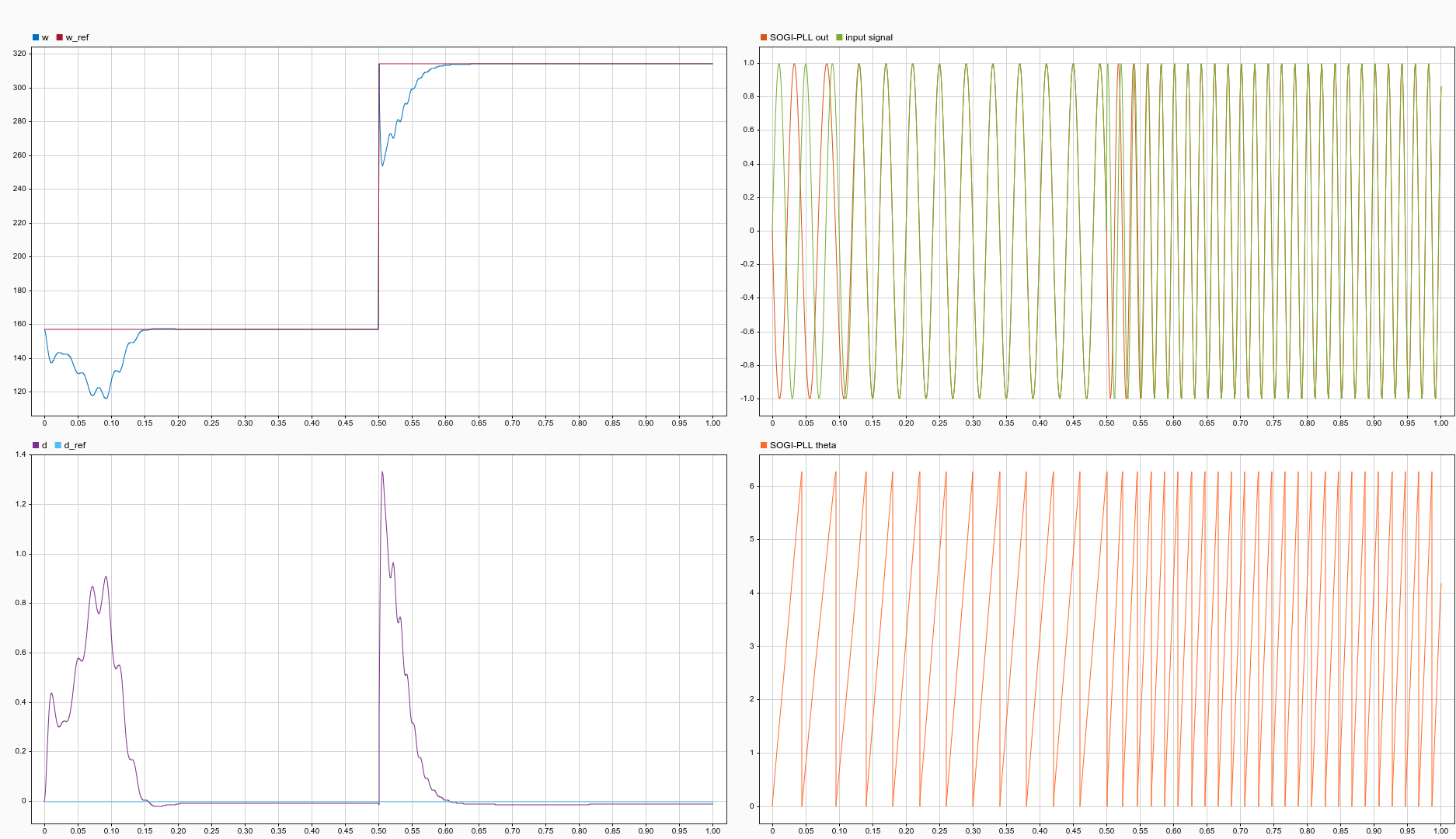
对SOGI单相锁相环有兴趣,可以参考文献9,该文献对SOGI单相锁相环写的清晰明了,图文并茂。
最近用C语言写了一个SogiPll锁相环,并实现了锁相功能,其实验波形请见图23。
锁相环的性能指标
- 稳态相角误差 state phase-angle error
- 相角响应速度 speed of response to angle
- 频率响应速度 speed of response to frequency
- 变频的适应能力 variable frequency rejection
- 谐波适应能力 harmonic rejection
- 非平衡电网适应能力 line unbalance rejection
推荐阅读有关PLL文献
Performance evaluation of PLL algorithms for single-phase grid-connected systems
Decoupled Double Synchronous Reference Frame PLL for Power Converters Control
Comparison of Three Single-Phase PLL Algorithms for UPS Applications
PLL structures for utility connected systems
A phase tracking system for three phase utility interface inverters
Operation of a phase locked loop system under distorted utility conditions
A new single-phase PLL structure based on second order generalized integrator
A new phase-locked loop (PLL) system
备注
I would greatly appreciate hearing about any error in this article, even minor ones. I welcome your suggestions for improvements, even tiny one. Please contact me by email 😜! Have fun!
参考文献
张崇巍, 张兴. PWM 整流器及其控制 [M]. 北京: 机械工业出版社, 2012.↩︎
KAURA V, BLASKO V. Operation of a phase locked loop system under distorted utility conditions[J]. IEEE Transactions on Industry applications, 1997, 33(1): 58-63.↩︎
CHUNG S K. A phase tracking system for three phase utility interface inverters[J/OL]. IEEE Transactions on Power electronics, 2000, 15(3): 431-438. DOI: 10.1109/63.844502.↩︎
LEE S J, KANG J K, SUL S K. A new phase detecting method for power conversion systems considering distorted conditions in power system[C/OL]//Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting (Cat. No.99CH36370):volume 4. 1999: 2167-2172 vol.4. DOI: 10.1109/IAS.1999.798754.↩︎
RODRIGUEZ P, POU J, BERGAS J, et al. Decoupled double synchronous reference frame pll for power converters control[J/OL]. IEEE Transactions on Power Electronics, 2007, 22(2):584-592. DOI: 10.1109/TPEL.2006.890000.↩︎
KARIMI-GHARTEMANI M, IRAVANI M R. A method for synchronization of power electronic converters in polluted and variable-frequency environments[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1263-1270.↩︎
SILVA S M, LOPES B M, CAMPANA R P, et al. Performance evaluation of pll algorithms for single-phase grid-connected systems[C]//Conference Record of the 2004 IEEE Industry Applications Conference, 2004. 39th IAS Annual Meeting.: volume 4. IEEE, 2004: 2259-2263.↩︎
FRANCIS B A, WONHAM W M. The internal model principle for linear multivariable regulators[J]. Applied mathematics and optimization, 1975, 2(2): 170-194.↩︎
CIOBOTARU M, TEODORESCU R, BLAABJERG F. A new single-phase pll structure based on second order generalized integrator[C/OL]//2006 37th IEEE Power Electronics Specialists Conference. 2006: 1-6. DOI: 10.1109/pesc.2006.1711988.↩︎

